Question

A Velocity-time graph for a body of mass 10 kg is shown in figure. Work-done on the body in first two seconds of the motion is :

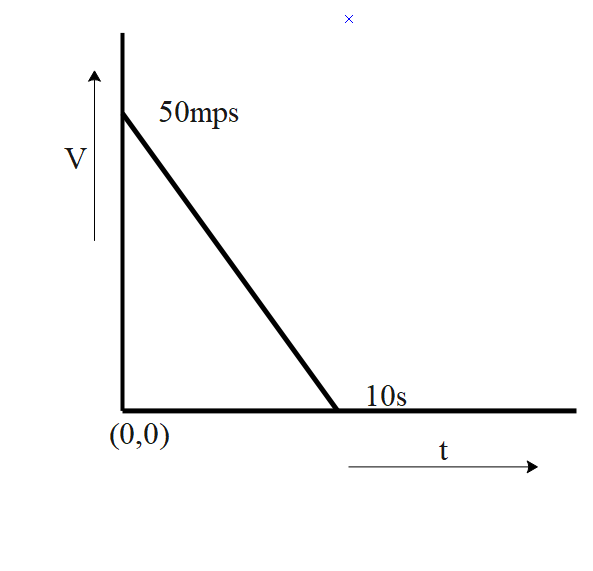
A) -9300J
B) 12000J
C) -4500J
D) -12000J

Answer 1

Let us find the equation of the velocity changing with respect to time as given in the graph in the question. Next, let us find the velocity at time t-2sec. Next, we know, the work done is equal to the change in kinetic energy, the final velocity of the body is at t=-2sec and initial velocity will be at t=0sec. Therefore, we can find the kinetic energy, thus, finding the work done easily.

Formula used: $W=\Delta K.E=\dfrac{1}{2}m{{v}^{2}}$

Complete step by step answer:
Let us find the velocity equation that is changing with respect to time,
We can write the equation as y=mx+c as it is a straight line, where y is velocity and x are time.
The slope is equal to -5 and the constant c=50
Now, the velocity that changes with respect to time will be,
$v=-5t+50$
Now, the velocity at time t=2sec will be,
${{v}_{t=2\sec }}=40$
Therefore, the change in kinetic energy will be,
$\begin{aligned} & \Delta K.E=\dfrac{1}{2}m{{v}^{2}} \\\ & \Delta K.E=\dfrac{1}{2}\times 10\times ({{40}^{2}}-{{50}^{2}}) \\\ & \Delta K.E=-4500J \\\ \end{aligned}$
As the change in kinetic energy is equal to the work done bin the system,
The work done is -4500J.

So, the correct answer is “Option C”.

Additional Information: The work-energy theorem states that the work done by all forces acting on a particle equals the change in the particle’s kinetic energy. Work transfers energy from one place to another or one form to another. In more general systems than the particle system mentioned here, work can change the potential energy of a mechanical device, the heat energy in a thermal system, or the electrical energy in an electrical device. The principle of work and kinetic energy (also known as the work-energy theorem) states that the work done by the sum of all forces acting on a particle equals the change in the kinetic energy of the particle. This definition can be extended to rigid bodies by defining the work of the torque and rotational kinetic energy.

Note: In the above question, the kinetic energy can be found from the graph given. Also, the initial velocity is taken at t=0sec and the work done is obtained as negative because the velocity is decreasing gradually as time is increasing. Due to this, kinetic energy decreases, resulting in the decrease of work done.