Question

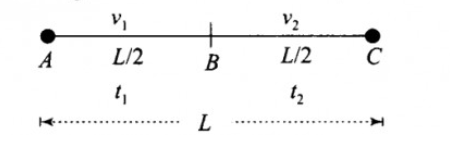
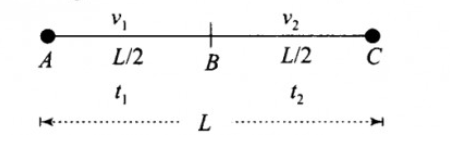
A vehicle travels half the distance L with speed ${v_1}$ and the other half with speed${v_2}$. What is the average speed?

Answer 1

Average speed is referred to as the speed for the whole journey. The ratio of the total distance traveled and the total time taken for the distance to be traveled is called average speed. This average speed definition must be applied to calculate the average speed.

Complete step-by-step solution:
The speed is defined as the ratio of the distance (d) traveled per unit time (t).
$s = \dfrac{d}{t}$

The term average speed(S) gives us a sense of the rate at which the journey is covered. It also represents the arithmetic mean of all the values of speed that the body travels over a distance.
If a body covers ${d_1}$the distance in time${t_1}$ , ${d_2}$ distance in time ${t_2}$ , and so on, and then the expression of average speed is,
$S = \dfrac{{{d_1} + {d_2} + ....}}{{{t_1} + {t_2} + ....}}$
Let us consider, D be the total distance traveled by the vehicle. $L$ is equal to one-half of this distance traveled.
Hence,
$L = \dfrac{D}{2}$
Total distance in terms of $L$ is
$D = 2L$
Total distance traveled by car on each trip –$L$
If the forward journey takes place with the speed of ${v_1}$, then the time taken for the journey is
${t_1} = \dfrac{L}{{{v_1}}}$
If the other half of the journey takes place with the speed of${v_2}$, then the time taken for the journey is
${t_2} = \dfrac{L}{{{v_2}}}$
The average speed for the journey,
$S = \dfrac{D}{{{t_1} + {t_2}}}$
Substituting the values, we have
$S = \dfrac{{2L}}{{\dfrac{L}{{{v_1}}} + \dfrac{L}{{{v_2}}}}}$
$\Rightarrow S = \dfrac{{2L}}{{\dfrac{{L{v_1} + L{v_2}}}{{{v_1}{v_2}}}}}$
$\Rightarrow S = \dfrac{{2L{v_1}{v_2}}}{{L({v_1} + {v_2})}}$
$\Rightarrow S = \dfrac{{2{v_1}{v_2}}}{{{v_1} + {v_2}}}$

Note: We can see from the solution of this problem that the average speed does not include the value of L. So, we can say that the total average speed is mainly dependent on the velocities irrespective of the distance covered in these speeds.