Question

A vehicle is at rest on a banked road with angle of banking $\theta$. The normal reaction of the angle is $N1$. When the vehicle takes a turn on the same road the normal reaction is $N2$. Then $\dfrac{{N1}}{{N2}}$ is equal to
A. $1$
B. ${\sin ^2}\theta$
C. ${\cos ^2}\theta$
D. $0.5\sin 2\theta$

Answer 1

Hint:- When the outer part of the road is raised a little above the inner part of the road in order to take a turn along the circular track is called banking of the road. The inclined track makes an angle $\theta$ with the horizontal. This angle is called angle of banking.

Complete step-by-step solution :Step I:

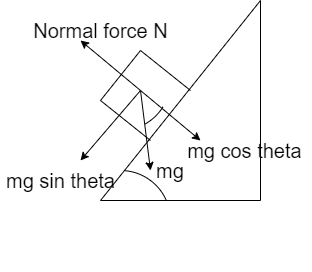
The normal component of force acting perpendicular to the plane is given by
$N1 = mg\cos \theta$---(i)

When it takes a normal turn on the road, the centripetal force is given by $\dfrac{{m{v^2}}}{r}$.
Step II:
Balancing the forces,
$mg\sin \theta = \dfrac{{m{v^2}}}{r}\cos \theta$
$\dfrac{{g\sin \theta }}{{\cos \theta }} = \dfrac{{{v^2}}}{r}$
Step III:
$N2 = mg\cos \theta + \dfrac{{m{v^2}}}{r}\sin \theta$
Substitute the value of $\dfrac{{{v^2}}}{r}$ in the above equation,
$N2 = mg\cos \theta + mg\tan \theta \sin \theta$---(ii)
Step IV:
Dividing equation (i) and (ii) to find the ratio,
$\dfrac{{N1}}{{N2}} = \dfrac{{mg\cos \theta }}{{mg\cos \theta + mg\tan \theta \sin \theta }}$
$\dfrac{{N1}}{{N2}} = \dfrac{{mg\cos \theta }}{{mg(\cos \theta + \tan \theta \sin \theta )}}$
$\dfrac{{N1}}{{N2}} = \dfrac{{\cos \theta }}{{\cos \theta + \tan \theta \sin \theta }}$
$\dfrac{{N1}}{{N2}} = \dfrac{{\cos \theta }}{{\cos \theta + \dfrac{{{{\sin }^2}\theta }}{{\cos \theta }}}}$
$\dfrac{{N1}}{{N2}} = \dfrac{{\cos \theta }}{{\dfrac{{{{\cos }^2}\theta + {{\sin }^2}\theta }}{{\cos \theta }}}}$
$\dfrac{{N1}}{{N2}} = \dfrac{{{{\cos }^2}\theta }}{1}$
$\dfrac{{N1}}{{N2}} = {\cos ^2}\theta$
Step V:
The ratio is equal to ${\cos ^2}\theta$.
Hence Option C is the right answer.

Note:- It is to be noted that when the road is banked the horizontal component of the normal provides the required centripetal force for circular motion of the car. The centripetal force can be increased if the road is made rough. The centripetal force is provided by the frictional force between the wheels of the car and the surface of the road.