Question

A vector with magnitude of 3 units, which is perpendicular to each of the vectors $\bar{a} = 3i+j-4k$ and $\bar{b} = 6i +5j - 2k$ is given by

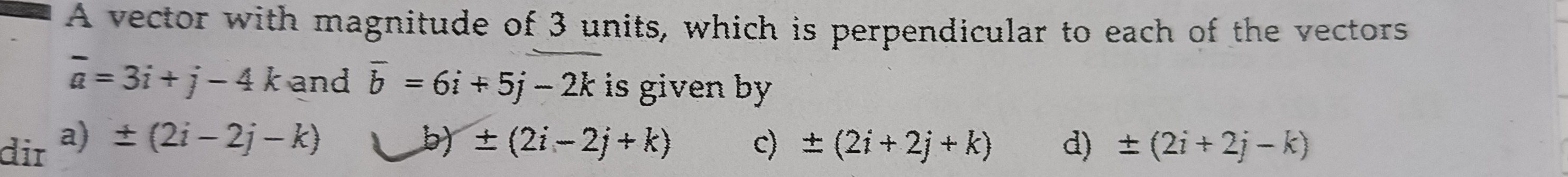
• A. ± (2i-2j-k)
• B. ± (2i-2j+k)
• C. ± (2i+2j+k)
• D. ± (2i+2j-k)

Answer 1

Answer: (B)

± (2i - 2j + k)

Answer 2

To find a vector perpendicular to both $\bar{a}$ and $\bar{b}$, we compute their cross product:

$\bar{a} \times \bar{b} = \begin{vmatrix} \mathbf{i} & \mathbf{j} & \mathbf{k} \\ 3 & 1 & -4 \\ 6 & 5 & -2 \end{vmatrix} = \mathbf{i}(1 \cdot (-2) - (-4 \cdot 5)) - \mathbf{j}(3 \cdot (-2) - (-4 \cdot 6)) + \mathbf{k}(3 \cdot 5 - 1 \cdot 6) = 18\mathbf{i} - 18\mathbf{j} + 9\mathbf{k} = 9(2\mathbf{i} - 2\mathbf{j} + \mathbf{k})$

The resulting vector is proportional to $2\mathbf{i} - 2\mathbf{j} + \mathbf{k}$.

Now, we need to scale this vector to have a magnitude of 3. The magnitude of $2\mathbf{i} - 2\mathbf{j} + \mathbf{k}$ is:

$\sqrt{2^2 + (-2)^2 + 1^2} = \sqrt{4 + 4 + 1} = \sqrt{9} = 3$

Since the magnitude is already 3, the required vector is $\pm (2\mathbf{i} - 2\mathbf{j} + \mathbf{k})$.