Solveeit Logo
Login

Question

Question: A vector of length l is turned through the angle \(\theta \) about its tail. What is the magnitude c...

A vector of length l is turned through the angle θ\theta about its tail. What is the magnitude change in the position vector of its head?
A. lcos⁡(θ/2)l\cos (\theta /2)
B. 2lsin⁡(θ/2)2l\sin (\theta /2)
C. 2lcos⁡(θ/2)2l\cos (\theta /2)
D. lsin⁡(θ/2)l\sin (\theta /2).

Explanation

Solution

Hint: In this question, we will use the concept of mathematical operations on vectors. Here we will use the parallelogram law of vector addition i.e. R=P2+Q2+2PQcos⁡θR = \sqrt {{P^2} + {Q^2} + 2PQ\cos \theta } .
Formula used: R=P2+Q2+2PQcos⁡θR = \sqrt {{P^2} + {Q^2} + 2PQ\cos \theta } .

Complete step-by-step solution -
__
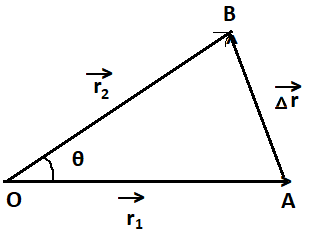
Given that, length of vector = l, angle inclined =θ\theta .
We have to find the magnitude change in the position of the vector.
We know that, if two vectors can be represented in both magnitude and direction by the two adjacent sides of a parallelogram drawn from a common point, ten their resultant is completely represented both in magnitude and direction by the diagonal of the parallelogram passing through that point.
According to the question, the vector is turned through the angle θ\theta about its tail. So the magnitude of resultant will become △r→=r2→−r1→\overrightarrow {\vartriangle r} = \overrightarrow {{r_2}} - \overrightarrow {{r_1}} , where r1=r2=l{r_1} = {r_2} = l
Using the parallelogram law of vector addition,
The magnitude of resultant vector, △r=r12+r22−2(r1)(r2)cos⁡θ\vartriangle r = \sqrt {{r_1}^2 + {r_2}^2 - 2({r_1})({r_2})\cos \theta }
⇒△r=2l2−2l2cos⁡θ\Rightarrow \vartriangle r = \sqrt {2{l^2} - 2{l^2}\cos \theta }
Now taking common 2l22{l^2} from both sides, we get
⇒△r=2l2(1−cos⁡θ)\Rightarrow \vartriangle r = \sqrt {2{l^2}(1 - \cos \theta } )
Using the identity, (1−cos⁡θ)=2sin⁡2θ2(1 - \cos \theta ) = 2{\sin ^2}\dfrac{\theta }{2}, we get
⇒△r=l2(2sin⁡2θ2) ⇒△r=2lsin⁡(θ2).  \Rightarrow \vartriangle r = l\sqrt {2\left( {2{{\sin }^2}\dfrac{\theta }{2}} \right)} \\\ \Rightarrow \vartriangle r = 2l\sin \left( {\dfrac{\theta }{2}} \right). \\\
Hence, we can see that the magnitude change in the position vector of its head = 2lsin⁡(θ2).2l\sin \left( {\dfrac{\theta }{2}} \right).
Therefore, the correct answer is option (B).

Note: Whenever we ask such a question, first we have to remember the concept of addition of vectors. Then we will use that method to find out the magnitude of the resultant vector when the magnitude of two vectors is given and the angle inclined is also given. Through this we will get the answer.