Question

A vector a has magnitude 5 units and points north east and another vector b has magnitude 5 units and points north west. Then the magnitude of the vector (a-b) is ?

1. 0
2. $5\sqrt 2$
3. 10
4. 25

Answer 1

A vector is an object which has both magnitudes and direction and is usually represented by an arrow. Here, we are given $\overrightarrow a = 5$ units which point north east and $\overrightarrow b = 5$ units which point north west. And, we need to find the value of $|\overrightarrow a - \overrightarrow b |$ . For this, we will draw the diagram first, and then we will get the value of vector a and vector b. Then, after using these values we can find the final output.

Complete answer:
Given that,
$\overrightarrow a$ has magnitude 5 units and points north east and
$\overrightarrow b$ has magnitude 5 units and points northwest.
According to the given information, we will draw a figure as below:

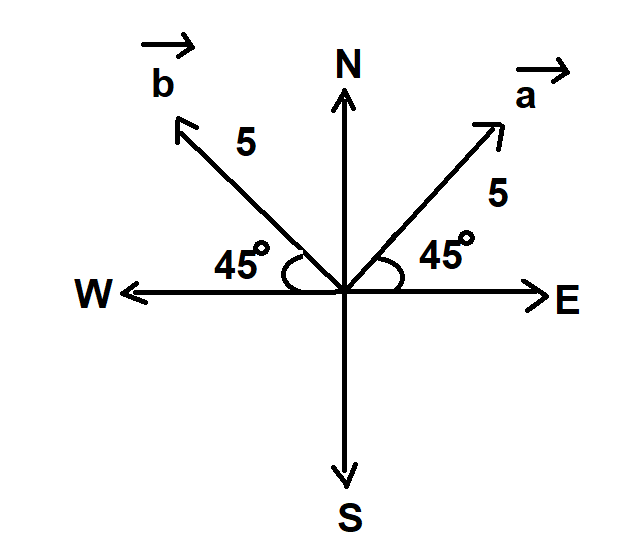
From the figure, we get,
$\overrightarrow a = 5\cos {45^\circ }\widehat i + 5\sin {45^\circ }\widehat j$
$\therefore \overrightarrow a = 5(\dfrac{1}{{\sqrt 2 }})\widehat i + 5(\dfrac{1}{{\sqrt 2 }})\widehat j$
$\therefore \overrightarrow a = \dfrac{5}{{\sqrt 2 }}(\widehat i + \widehat j)$
And,
$\overrightarrow b = 5\cos {45^\circ }( - \widehat i) + 5\sin {45^\circ }\widehat j$
$\therefore \overrightarrow b = 5(\dfrac{1}{{\sqrt 2 }})( - \widehat i) + 5(\dfrac{1}{{\sqrt 2 }})\widehat j$
$\therefore \overrightarrow b = \dfrac{5}{{\sqrt 2 }}( - \widehat i + \widehat j)$
We need to find the magnitude of vector (a-b), which is done as below:
$\therefore \overrightarrow a - \overrightarrow b$
$= \dfrac{5}{{\sqrt 2 }}(\widehat i + \widehat j) - \dfrac{5}{{\sqrt 2 }}( - \widehat i + \widehat j)$
$= \dfrac{5}{{\sqrt 2 }}(\widehat i + \widehat j) - \dfrac{5}{{\sqrt 2 }}( - \widehat i + \widehat j)$
$= \dfrac{5}{{\sqrt 2 }}\widehat i + \dfrac{5}{{\sqrt 2 }}\widehat j + \dfrac{5}{{\sqrt 2 }}\widehat i - \dfrac{5}{{\sqrt 2 }}\widehat j$
$= \dfrac{5}{{\sqrt 2 }} \times 2\widehat i$
$= 5\sqrt 2 \widehat i$
$\therefore |\overrightarrow a - \overrightarrow b | = 5\sqrt 2$

Another Method:
Given that,
$|\overrightarrow a | = 5$ units and $|\overrightarrow b | = 5$ units
$\therefore |\overrightarrow a - \overrightarrow b |$
$= \sqrt {|a{|^2} + |b{|^2} + 2|a||b|\cos \theta }$
$= \sqrt {{5^2} + {5^2} + 2(5)(5)\cos {{90}^\circ }}$
$= \sqrt {25 + 25 + 2(5)(5)(0)}$ $(\because \cos {90^\circ } = 0)$
$= \sqrt {25 + 25 + 2(5)(5)(0)}$
$= \sqrt {25 + 25 + 0}$
$= \sqrt {50 + 0}$
$= \sqrt {50}$
$= \sqrt {5 \times 5 \times 2}$
$= 5\sqrt 2$
Hence, for the given $\overrightarrow a = 5$ units which points north east and $\overrightarrow b = 5$ units which points north west, then the value of $|\overrightarrow a - \overrightarrow b | = 5\sqrt 2$ .

Note:
Vector algebra studies the algebra of vector quantities. There are two types of physical quantities, scalars and vectors. The scalar quantity has only magnitude, whereas the vector quantity has both magnitude and direction. The magnitude of the vector is represented as |V|. Two vectors are said to be equal if they have equal magnitudes and equal direction. We also perform arithmetic operations such as addition, subtraction, multiplication on vectors. But, in the case of multiplication, vectors have two terminologies, such as dot product and cross product.