Question

A variable triangle is inscribed in a circle of radius R . If the rate of change side is R times the rate of change of opposite angle , then the angle is
A) $\dfrac{\pi }{6}$
B) $\dfrac{\pi }{4}$
C) $\dfrac{\pi }{3}$
D) $\dfrac{\pi }{2}$

Answer 1

Use sine rule formula $\dfrac{a}{{\sin A}} = \dfrac{b}{{\sin B}} = \dfrac{c}{{\sin C}} = 2R$ here a , b , c are the sides of the triangle at a particular instant where $\angle A,\angle B,\angle C$ are the corresponding opposite angles to the sides a , b , c at a particular instant and R is the radius of the circumcircle.Form an equation from the data given in the question and substitute the value from the sine rule formula and get the required answer.

Complete step-by-step answer:
Let us construct a circle of radius R and a triangle ABC inscribed in it of variable sides da , db , dc
At a particular instant it has sides a , b , c

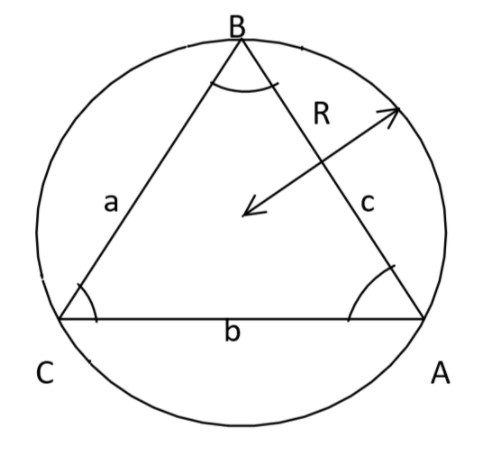
From the question it is given that If the rate of change side is R times the rate of change of opposite angle
$\dfrac{{d(side)}}{{dt}} = R \times \dfrac{{d(angle)}}{{dt}}$
Let us consider side a and its corresponding opposite angle $\angle A$
$\therefore$ we can obtain the equation
$\dfrac{{d(a)}}{{dt}} = R \times \dfrac{{d(\angle A)}}{{dt}}------------(1)$
Considering a , b , c as the sides of the triangle at a particular instant
Using sine rule $\dfrac{a}{{\sin A}} = \dfrac{b}{{\sin B}} = \dfrac{c}{{\sin C}} = 2R$
$\because$ we are considering side a and $\angle A$
we would obtain a simplified formula $a = 2R\sin A---(2)$
differentiating equation 2 on both sides with respect to time
$\dfrac{{d(a)}}{{dt}} = \dfrac{{d(2R\sin A)}}{{dt}}$
Since we know differentiation of constant is zero
$\dfrac{{d(a)}}{{dt}} = 2R\dfrac{{d(\sin A)}}{{dt}}$
Differentiation of $\sin A = \cos A$
$\dfrac{{d(a)}}{{dt}} = 2R\cos A\dfrac{{d(A)}}{{dt}}---- (3)$
By equating equation 1 and equation 3 we get
$R\dfrac{{d(A)}}{{dt}} = 2R\cos A\dfrac{{d(A)}}{{dt}}$
Cancelling R and $\dfrac{{dA}}{{dt}}$ terms on both the sides
$1 = 2\cos A$
$\therefore \cos A = \dfrac{1}{2}$
$A = {\cos ^{ - 1}}(\dfrac{1}{2})$
$\therefore$ we know ${\cos ^{ - 1}}(\dfrac{1}{2}) = \dfrac{\pi }{3}$
$\therefore \angle A = \dfrac{\pi }{3}$
Therefore for the variable triangle having side a, b , c for the side its opposite angle $\angle A$ will be equal to 60 degrees.

So, the correct answer is “Option C”.

Note: In the above problem we took the reference of side a and the corresponding opposite angle $\angle A$ but we can also take the reference of side b and side c and their corresponding opposite angles $\angle B,\angle C$.Students should remember the sine rule formula for solving these types of problems.