Question
Question: A variable resistor \[R\] is wired into a circuit shown below. To what value should this variable re...
A variable resistor R is wired into a circuit shown below. To what value should this variable resistor be set to generate 0.9A of current passing through the 10Ω resistor?
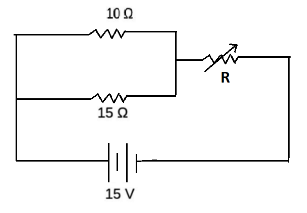
Solution
Calculate voltage across the 10Ω resistor as the current is given. This voltage is equal to that, passing through the resistor 15Ω as both the resistors are parallel in connection. From there obtain the current. Calculate the total current. Now apply Kirchhoff's law to calculate the variable resistor.
Complete answer:
Given,
V=15Volt
A current of 0.9A passes through the 10Ω resistor.
Let,
I1=0.9A
R1=10Ω
Voltage (V1) across this resistor can be obtained by using Ohm’s law.
Therefore, V1=I1R1 …… (1)
Substitute I1=0.9A and R1=10Ω in equation (1).
\Rightarrow {V_1} = 0.9 \times 10 \\\
\Rightarrow {V_1} = 9\,\,{\text{Volt}} \\\
Since, 15Ω resistor is parallel to 10Ω resistor. Therefore, voltage across the 15Ω resistor will be also 9Volt .
Let, the current across this resistor is I2
R2=15Ω
Now, current I2 is obtained by using Ohm’s law.
i.e. I2=R2V1 …… (2)
Substitute V1=9Volt and R2=15Ω in equation (2).
\Rightarrow {I_2} = \dfrac{9}{{15}} \\\
\Rightarrow {I_2} = 0.6\,\,{\text{A}} \\\
Now total current in the circuit is calculated by,
I = {I_1} + {I_2} \\\
\Rightarrow I = 0.9 + 0.6 \\\
\Rightarrow I = 1.5\,\,{\text{A}} \\\
Now this total current I=1.5A flows across the variable resistor R.
Now we apply Kirchhoff’s law for the closed mesh,
V=10I1+IR ….. (3)
Substitute V=15Volt, I1=0.9A and I=1.5A in equation (3).
Therefore,
\Rightarrow 15 = \left( {10 \times 0.9} \right) + 1.5R \\\
\Rightarrow 15 = 9 + 1.5R \\\
\Rightarrow 1.5R = 15 - 9 \\\
\Rightarrow R = \dfrac{6}{{1.5}} \\\
∴R=4Ω
Hence, the value of the variable resistor is 4ohms.
Note: From the diagram we can see that the resistors 10Ω and 15Ω are parallel in connection. Therefore, the voltage drops across it will be equal. It is where most of the students seem to be confused about the connections of the resistors. In series connection, the same amount of current flows through all the elements.
According to ohm’s law, the current between the two points through a conductor is directly proportional to the voltage between the two points. The formula is given by, V=IR. Using this equation, we calculate the respective voltages and the currents. In every closed loop network, the overall voltage across the loop is equivalent to the total of all of the voltage drops inside the same loop, and is also equal to zero. This law is known as Kirchhoff’s Voltage Law or KVL.
