Question

A variable parabola of latus rectum $\Psi$ touches a fixed equal parabola then axis of the two curves are parallel. The locus of the vertex of the moving curve is a parabola whose latus rectum is
(a) $\Psi$
(b) $2\Psi$
(c) $4\Psi$
(d) None of these

Answer 1

Hint : To solve this question first of all assume an equation of given parabola as ${{y}^{2}}=4ax$ then $\Psi =4a$. Now from this try to determine the equation of other equal parabola by using vertex $\left( \alpha ,\beta \right)$. Finally from these two parables and equations of them determine the equation of the third parabola. Lastly compare the equation of third parabola to first parabola to get eh latus rectum.

Complete step-by-step answer :
Given that we have a parabola ${{y}^{2}}=4ax$ - (1), whose latus rectum is $\Psi =4a$.
Now given that there is another fixed equal parabola, then it would be having the same latus rectum $\Psi$ (as it is given that both are equal parabolas).
Now because the axes are parallel and they touch each other.
Then the locus of the parabola would be of the form,
${{\left( y-\beta \right)}^{2}}=-4a\left( x-\alpha \right)$ - (2)
This is the equation of parabola with vertex $\left( \alpha ,\beta \right)$. Here “4a” is the same because they are equal parabolas. Now given that the both parabola are touching, then if the original parabola would be like,

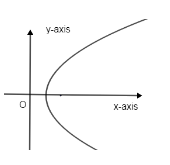
Then the new parabola would be of the form,

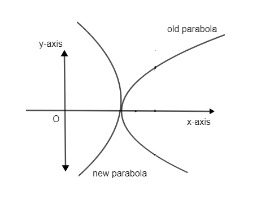
Hence we have a negative sign in ‘4a’ of equation (2) of new parabola,
Now we will solve equation (1) & (2) to get required result;

& {{y}^{2}}=4ax \\\ & \Rightarrow \dfrac{{{y}^{2}}}{4a}=x\Rightarrow x=\dfrac{{{y}^{2}}}{4a} \\\ \end{aligned}$$ Substituting this value of equation (1) to equation (2) we get; $${{\left( y-\beta \right)}^{2}}=-4a\left( \dfrac{{{y}^{2}}}{4a}-\alpha \right)$$ Opening square we have, $$\begin{aligned} & \Rightarrow {{y}^{2}}-2\beta y+{{\beta }^{2}}=-{{y}^{2}}+4a\alpha \\\ & \Rightarrow 2{{y}^{2}}-2\beta y+{{\beta }^{2}}-4a\alpha =0 \\\ \end{aligned}$$ Now because they only touch each other and therefore roots are real. Hence we have discriminant, D = 0. $$\begin{aligned} & \Rightarrow D=0 \\\ & \Rightarrow 4{{\beta }^{2}}-4.2\left( {{\beta }^{2}}-4a\alpha \right)=0 \\\ \end{aligned}$$ Simplifying we get, $$\begin{aligned} & \Rightarrow 4{{\beta }^{2}}-8{{\beta }^{2}}+32a\alpha =0 \\\ & \Rightarrow -4{{\beta }^{2}}=-32a\alpha \\\ & \Rightarrow {{\beta }^{2}}=8a\alpha \\\ \end{aligned}$$ Now $$\left( \alpha ,\beta \right)$$ are co – ordinates of vertex. Then general co – ordinates are (x, y). So replace we have, $${{y}^{2}}=8ax$$ Now the original parabola and latus rectum = $$\Psi =4a$$. Then the new parabola has latus rectum $$\Rightarrow 8a=2\Psi $$. $$\Rightarrow $$ The latus rectum of the new parabola is $$2\Psi $$. **So, the correct answer is “Option B”.** **Note** : The possibility of error in this question can be not determining the equation of the third parabola and directly going to determine the latus rectum of it, which would be wrong because even if it is given in the question that the locus forms a parabola, we need to determine the equation also.