Question

A variable circle passes through a fixed point $A\left( p,q \right)$ and touches the X-axis. The locus of the other end of the diameter thorough A is
A. ${{\left( x-p \right)}^{2}}=4qy$
B. ${{\left( x-q \right)}^{2}}=4py$
C. ${{\left( y-p \right)}^{2}}=4qx$
D. ${{\left( y-q \right)}^{2}}=4px$

Answer 1

We first take the general form of the circle and find the condition for it touching the X-axis. We take the other end of the diameter and use the centre to place the points in the equation. The new form gives us the locus for the other end of the diameter.

Complete answer:
The general equation of a circle is ${{\left( x+g \right)}^{2}}+{{\left( y+f \right)}^{2}}={{r}^{2}}$ with $O\left( -g,-f \right)$ being centre and $r$ being the radius.
As the circle touches X-axis, the y coordinate of the centre becomes the radius. So, ${{r}^{2}}={{f}^{2}}$.
$\begin{aligned} & {{\left( x+g \right)}^{2}}+{{\left( y+f \right)}^{2}}={{r}^{2}} \\\ & \Rightarrow {{\left( x+g \right)}^{2}}+{{\left( y+f \right)}^{2}}={{f}^{2}} \\\ & \Rightarrow {{\left( x+g \right)}^{2}}+{{y}^{2}}+2fy=0 \\\ \end{aligned}$
The point $A\left( p,q \right)$ passes through the circle ${{\left( x+g \right)}^{2}}+{{y}^{2}}+2fy=0$.
So, ${{\left( p+g \right)}^{2}}+{{q}^{2}}+2fq=0$.
Now let us assume the other end of the diameter thorough $A\left( p,q \right)$ is $B\left( h,k \right)$.

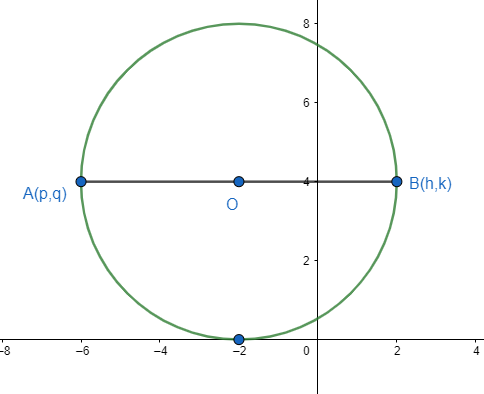
Therefore, the middle point of the points $A\left( p,q \right)$ and $B\left( h,k \right)$ is $O\left( -g,-f \right)$.
The formula gives us $\dfrac{p+h}{2}=-g$ and $\dfrac{q+k}{2}=-f$. We get $2f=-\left( q+k \right)$.
We put the values in the equation of ${{\left( p+g \right)}^{2}}+{{q}^{2}}+2fq=0$.
$\begin{aligned} & {{\left( p+g \right)}^{2}}+{{q}^{2}}+2fq=0 \\\ & \Rightarrow {{\left( p-\dfrac{p+h}{2} \right)}^{2}}+{{q}^{2}}-q\left( q+k \right)=0 \\\ \end{aligned}$
We now simplify the equation to get the locus.
$\begin{aligned} & {{\left( p-\dfrac{p+h}{2} \right)}^{2}}+{{q}^{2}}-q\left( q+k \right)=0 \\\ & \Rightarrow {{\left( \dfrac{p-h}{2} \right)}^{2}}+{{q}^{2}}-{{q}^{2}}-qk=0 \\\ & \Rightarrow \dfrac{{{\left( p-h \right)}^{2}}}{4}=qk \\\ & \Rightarrow {{\left( h-p \right)}^{2}}=4qk \\\ \end{aligned}$
Now taking the conventional terms for $B\left( h,k \right)$ we get ${{\left( x-p \right)}^{2}}=4qy$. The correct option is A.

Note:
We need to remember the condition for touching the X or Y-axis for a circle. The conditions are ${{g}^{2}}=c$ and ${{f}^{2}}=c$ respectively for circle’s equation ${{x}^{2}}+2gx+{{y}^{2}}+2fy+c=0$.