Solveeit Logo
Login

Question

Question: A variable chord of the hyperbola $\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$ is tangent to the circle $x^2+...

A variable chord of the hyperbola x2a2−y2b2=1\frac{x^2}{a^2}-\frac{y^2}{b^2}=1 is tangent to the circle x2+y2=c2x^2+y^2=c^2. Prove that locus of its mid-point is (x2a2−y2b2)2=c2(x2a4+y2b4)\left(\frac{x^2}{a^2}-\frac{y^2}{b^2}\right)^2=c^2\left(\frac{x^2}{a^4}+\frac{y^2}{b^4}\right)

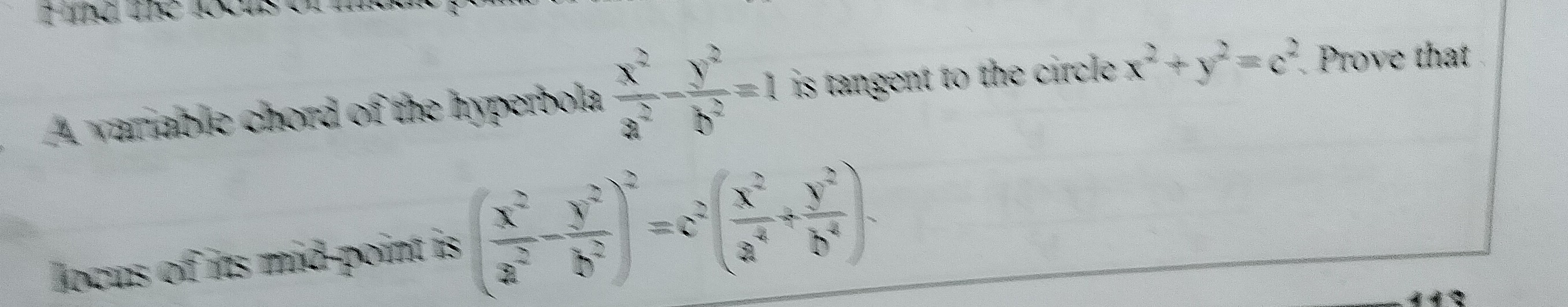
Answer

The locus of the midpoint is (x2a2−y2b2)2=c2(x2a4+y2b4)\left(\frac{x^2}{a^2}-\frac{y^2}{b^2}\right)^2=c^2\left(\frac{x^2}{a^4}+\frac{y^2}{b^4}\right).

Explanation

Solution

  1. The equation of the chord of the hyperbola x2a2−y2b2=1\frac{x^2}{a^2}-\frac{y^2}{b^2}=1 with midpoint (h,k)(h,k) is xha2−ykb2=h2a2−k2b2\frac{xh}{a^2}-\frac{yk}{b^2} = \frac{h^2}{a^2}-\frac{k^2}{b^2}.
  2. Rewriting this in the form Ax+By+C=0Ax+By+C=0, we get ha2x−kb2y−(h2a2−k2b2)=0\frac{h}{a^2}x - \frac{k}{b^2}y - \left(\frac{h^2}{a^2}-\frac{k^2}{b^2}\right) = 0.
  3. The condition for this chord to be tangent to the circle x2+y2=c2x^2+y^2=c^2 is that the perpendicular distance from the center (0,0)(0,0) to the chord equals the radius cc.
  4. This leads to the condition C2=c2(A2+B2)C^2 = c^2(A^2+B^2), where A=ha2A=\frac{h}{a^2}, B=−kb2B=-\frac{k}{b^2}, and C=−(h2a2−k2b2)C=-\left(\frac{h^2}{a^2}-\frac{k^2}{b^2}\right).
  5. Substituting these values gives (h2a2−k2b2)2=c2(h2a4+k2b4)\left(\frac{h^2}{a^2}-\frac{k^2}{b^2}\right)^2 = c^2\left(\frac{h^2}{a^4}+\frac{k^2}{b^4}\right).
  6. Replacing (h,k)(h,k) with (x,y)(x,y) yields the locus: (x2a2−y2b2)2=c2(x2a4+y2b4)\left(\frac{x^2}{a^2}-\frac{y^2}{b^2}\right)^2=c^2\left(\frac{x^2}{a^4}+\frac{y^2}{b^4}\right).