Question
Question: A value of x satisfying the equation $\sin [cot^{-1}(1 + x)] = \cos[tan^{-1}x]$, is...
A value of x satisfying the equation sin[cot−1(1+x)]=cos[tan−1x], is
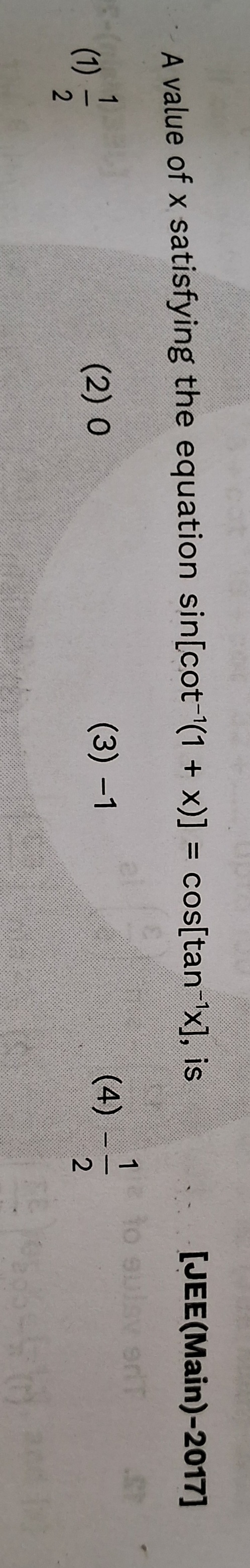
A
2−1
B
0
C
-1
D
-21
Answer
x = -21
Explanation
Solution
To solve the equation sin[cot−1(1+x)]=cos[tan−1x], we can use trigonometric identities.
First, we simplify both sides of the equation:
-
Left-hand side (LHS): sin[cot−1(1+x)]=1+(1+x)21
-
Right-hand side (RHS): cos[tan−1x]=1+x21
Now, we set the LHS equal to the RHS:
1+(1+x)21=1+x21
Squaring both sides to eliminate the square roots gives:
1+(1+x)2=1+x2
Expanding and simplifying:
1+(1+2x+x2)=1+x2 2+2x+x2=1+x2 2x=−1 x=−21
To verify the solution, we substitute x=−21 back into the original equation. Both sides evaluate to 52, confirming that x=−21 is indeed the correct solution.
