Question

A V shaped bent wire is carrying current I and ends of wire extends to infinity. If the magnetic field at P can be written as $K\tan (\dfrac{\alpha }{2})$, then K is

Angle a = $\alpha$

(A). $\dfrac{{{\mu }_{0}}I}{4\pi d}$
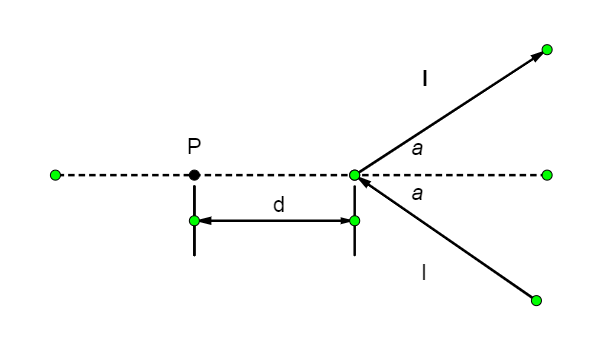
(B). $\dfrac{{{\mu }_{0}}I}{2\pi d}$
(C). $\dfrac{{{\mu }_{0}}I}{\pi d}$
(D). $\dfrac{2{{\mu }_{0}}I}{\pi d}$

Answer 1

Find the magnetic field of one segment by extending the segment forward and analyzing the angles. Two times this magnetic field gives the total magnetic field at point P. As the segment extends to infinity ${{\theta }_{1}}={{0}^{o}}$

Formulas used:
B=$\dfrac{{{\mu }_{0}}I}{4\pi D}(\cos {{\theta }_{1}}+\cos {{\theta }_{2}})$

Complete step-by-step answer:
Magnetic field due to a straight line= $\dfrac{{{\mu }_{0}}I}{4\pi D}(\cos {{\theta }_{1}}+\cos {{\theta }_{2}})$ ………. (1)

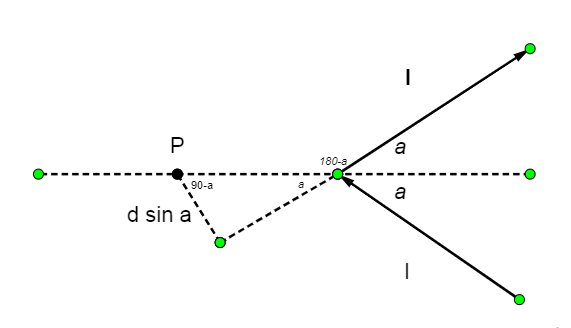
Angle a = $\alpha$

Here,
$D=d\sin \alpha$
${{\theta }_{1}}={{0}^{o}}$
${{\theta }_{2}}={{180}^{o}}-\alpha$
Let us substitute the above values in equation (1) and we get
$B=\dfrac{{{\mu }_{0}}I}{4\pi d\sin \alpha }(\cos {{0}^{o}}+\cos ({{180}^{o}}-\alpha ))$
$=\dfrac{{{\mu }_{0}}I}{4\pi (d\sin \alpha )}(1-cos\alpha )=\dfrac{{{\mu }_{0}}I}{4\pi d}\tan \dfrac{\alpha }{2}$ (Since$(\dfrac{1-\cos \alpha }{\sin \alpha })=\tan \dfrac{\alpha }{2}$)
Resultant field will be
$\dfrac{{{\mu }_{0}}I}{\pi d}$ ${{B}_{net}}=2B=\dfrac{{{\mu }_{0}}I}{2\pi d}\tan \dfrac{\alpha }{2}$
$\Rightarrow K=\dfrac{{{\mu }_{0}}I}{2\pi d}$ $\alpha$
Hence the correct option is (B).

Additional information:
Biot-Savart Law: An equation demonstrating the magnetic field generated by an electric current at any particular point is known as Biot-Savart Law equation. It relates the magnetic field to the magnitude, direction and length of the electric current carried in a wire. The law is valid in the magnetostatic standards, and is consistent with both Ampère’s law and Gauss’s law for magnetism.
The direction of magnetic field due to a straight current carrying wire can be demonstrated by the right hand thumb rule. Here the direction of the thumb represents the direction of current and the curl of the other fingers represents the direction of the magnetic field.

Note: The possibility of making a mistake is choosing option (a) because you may forget to calculate the net magnetic field by adding magnetic fields of both the segments. If you use the magnetic field of one segment and calculate K, you will obtain option (a). In this topic, it is important for the students to estimate the value of Ɵ which can ultimately decide the magnitude of the magnetic field.