Question

(a) Using Bohr’s postulates obtain the expression for total energy of the electron in the ${n^{th}}$ orbit of a hydrogen atom.
(b) What is the significance of negative sign in the expression for energy?
(c) Draw the energy level diagram showing how the line of spectra corresponding to Paschen series occur due to transition between energy levels

Answer 1

To find the total energy we will be using the postulates given by Bohr according to the need to find relationship between certain values so as to obtain the final result.
Total energy is equal to the sum of kinetic and potential energy and
Kinetic energy= $\dfrac{1}{2}m{v^2}$
The hydrogen spectrum shows the series after the electron transfers and there are fixed values of final energy levels for respective series formed.

Complete step by step answer: An electron is revolving around the nucleus of hydrogen atom can be represented diagrammatically as:

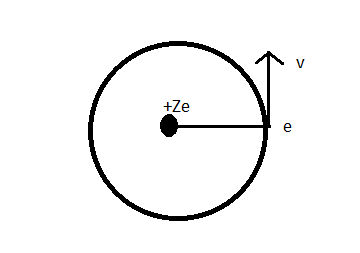
Let mass of electron = e [instead of taking value]
And mass of nucleus = Ze [Z = atomic number]
(a) According to Bohr’s postulate:
The centripetal force is provided to an electron revolving around the nucleus (positively charged) by the force of attraction between the nucleus and the electron.
The respective forces are given as:
Centripetal force = $\dfrac{{m{v^2}}}{r}$
Force of attraction = $\dfrac{{K(Ze)e}}{{{r^2}}}$ where K = $\dfrac{1}{{4\pi {\varepsilon _0}}}$
Then,
$\dfrac{{m{v^2}}}{r}$= $\dfrac{1}{{4\pi {\varepsilon _0}}}\dfrac{{(Ze)e}}{{{r^2}}}$ ____________ (1)
$m{v^2}$ = $\dfrac{1}{{4\pi {\varepsilon _0}}}\dfrac{{Z{e^2}}}{{{r^{}}}}$
Now,
Kinetic energy (K.E)= $\dfrac{1}{2}m{v^2}$
Substituting the value of $m{v^2}$ (calculated), we get:
K.E = $\dfrac{1}{{4\pi {\varepsilon _0}}}\dfrac{{Z{e^2}}}{{2r}}$
Potential energy (P.E) is given as:
P.E = $\dfrac{{K(Ze)( - e)}}{{{r^2}}}$
The total energy (T.E) is given by the sum of kinetic and potential energy.
T.E = K.E + P.E
T.E = $\left( {\dfrac{1}{{4\pi {\varepsilon _0}}}\dfrac{{Z{e^2}}}{{2r}}} \right) + \left( { - \dfrac{1}{{4\pi {\varepsilon _0}}}\dfrac{{Z{e^2}}}{{2r}}} \right)$
T.E = $- \dfrac{1}{{4\pi {\varepsilon _0}}}\dfrac{{Z{e^2}}}{{2r}}$
For ${n^{th}}$ orbit:
$T.{E_n} = - \dfrac{1}{{4\pi {\varepsilon _0}}}\dfrac{{Z{e^2}}}{{2{r_n}}}$ ____________ (2)
Bohr’s postulate for angular momentum (L) that states only the electrons with momentum $L = \dfrac{{nh}}{{2\pi }}$ are allowed.
In general angular momentum (L) is given as:
L = mvr
Equating the two, we get:
mvr = $\dfrac{{nh}}{{2\pi }}$
Finding the value of v:
$v = \dfrac{{nh}}{{2\pi mr}}$
Substituting this value of v in (1), we get:
$\dfrac{m}{r}{\left( {\dfrac{{nh}}{{2\pi mr}}} \right)^2} = \dfrac{1}{{4\pi {\varepsilon _0}}}\dfrac{{Z{e^2}}}{{{r^2}}}$

Calculating r for ${n^{th}}$ orbit:
${r_n} = \dfrac{{{\varepsilon _0}{h^2}{n^2}}}{{\pi mZ{e^2}}}$

Substituting this in (2), we get:
$T.{E_n} = - \dfrac{1}{{4\pi { \in _0}}}\dfrac{{Z{e^2}}}{{2\left( {\dfrac{{{\varepsilon _0}{h^2}{n^2}}}{{\pi mZ{e^2}}}} \right)}}$
$T.{E_n} = - \dfrac{m}{{8{\varepsilon _0}}}\dfrac{{{Z^2}{e^4}}}{{{h^2}{n^2}}}$
Therefore, using Bohr’s postulates the expression for total energy of the electron in the ${n^{th}}$ orbit of hydrogen atom is :
$T.{E_n} = - \dfrac{m}{{8{\varepsilon _0}}}\dfrac{{{Z^2}{e^4}}}{{{h^2}{n^2}}}$ ___________ (3)
This can also be written as:
$T.{E_n} = - \dfrac{{{Z^2}Rhc}}{{{n^2}}}$
Where,
R is called Rydberg constant and the value it takes is:
$R = \dfrac{m}{{8{\varepsilon _0}}}\dfrac{{{e^4}}}{{{h^3}c}}$
Now, Z = 1 for Hydrogen atom [Atomic number of Hydrogen is 1]
Therefore,
$T.{E_n} = - \dfrac{{Rch}}{{{n^2}}}$ __________ (4)
Thus the expression for total energy is ${n^{th}}$ orbit of hydrogen atom is :
$T.{E_n} = - \dfrac{{{Z^2}Rhc}}{{{n^2}}}$ or $T.{E_n} = - \dfrac{{Rch}}{{{n^2}}}$

(b) The negative sign obtained in the expression for total energy shows that electron is bounded to the nucleus by the force of attraction.

(c) In line spectra (of hydrogen), the different series are obtained when electrons jump from higher excited state $\left( {{n_i}} \right)$ to ground state $\left( {{n_f}} \right)$
Lymann series 🡪 ${n_f}$ = 1
Balmer series 🡪 ${n_f}$ = 2
Paschen series 🡪 ${n_f}$ = 3
Brackett series 🡪 ${n_f}$ = 4
Pfund series 🡪 ${n_f}$ = 5
For Paschen series (${n_f}$ = 3), the spectra is given as:

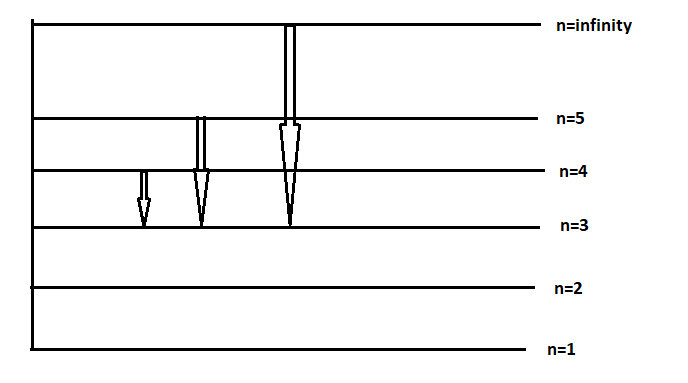
So during the transition the final energy level for electrons in the paschen series is n = 3.

Note: When we calculate potential energy, we take signs into consideration as well. (As we took negative for electron while calculating P.E)
Paschen series is the near to infrared
The change in energy $\left( {\Delta E} \right)$can also be calculated as:
$\Delta E = \dfrac{{m{e^4}}}{{8{\varepsilon ^2}_0{h^2}}}\left( {\dfrac{1}{{{n^2}_f}} - \dfrac{1}{{{n^2}_i}}} \right)$