Question

(a) Use Gauss’ law to derive the expression for the electric field $\left( {\vec E} \right)$ due to a straight uniformly charged infinite line of charge density $\lambda \,\left( {\dfrac{C}{m}} \right)$.
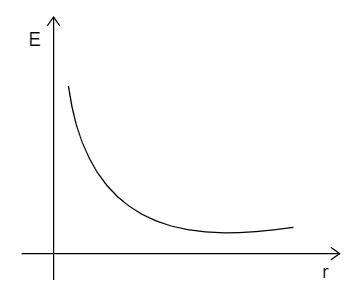
(b) Draw a graph to show the variation of $E$ with perpendicular distance $r$ from the line of charge.
(c) Find the work done in bringing a charge $q$ from perpendicular distance ${r_1}$ to ${r_2}\,\left( {{r_2} > {r_1}} \right)$.

Answer 1

Use the formula of the gauss law to calculate the electric field over a particular area. If the perpendicular distance between the line of charges increases, then its electric field decreases, based on this fact drawn from the graph. Use the work done formula and substitute the electric field and the other formula in it to find work done.

Formula used:
(1) The formula of the gauss law is
$\int {E.ds = \dfrac{{q\left( {enclosed} \right)}}{E}}$
Where $E$ is the electric field, $q$ is the charge and $ds$ is the area.
(2) Area of the cylinder is given by
$A = 2\pi rl$
$A$ is the area of the cylinder, $r$ is the radius of the cylinder and $l$ is the length of it.
(3) (c) Work done to bring the charge from the final distance is given by
$w = qv$
Where $q$ is the charge that is brought from the finite distance and $v$ is the voltage required.

Complete step by step solution:
(a) The gauss law states that the total electric flux over the enclosed surface is $\dfrac{1}{{{ \in _0}}}$ times the total charge in the surface.
$\int {E.ds = \dfrac{{q\left( {enclosed} \right)}}{E}}$
The area enclosed in the closed surface includes top, bottom and the curved area. But at the top of the bottom area, the electric field is perpendicular to the surface. Hence $\int {E.ds = 0}$. So only the curved surface is taken under consideration.
$\Rightarrow \int {E.ds = \dfrac{{\lambda L}}{E}}$
Since the taken area is the cylinder,
$\Rightarrow E\left( {2\pi RL} \right) = \dfrac{{\lambda L}}{E}$
By rearranging the obtained equation,
$\Rightarrow E = \dfrac{\lambda }{{2\pi ER}}$
Hence the electric field of the straight conductor is obtained as $\dfrac{{2K\lambda }}{R}$.
(b)

(c) Work done to bring the charge from the finite distance is calculated as follows
We know that the $v = Ed$

\Rightarrow {V_b} - {V_a} = \int_{{r_1}}^{{r_2}} { - {E_r}dr} \\\ \Rightarrow {V_b} - {V_a} = \int_{{r_1}}^{{r_2}} {\dfrac{\lambda }{{2\pi { \in _ \circ }r}}dr} \\\ \Rightarrow {V_b} - {V_a} = \dfrac{\lambda}{2 \pi \varepsilon _0} ln(\dfrac{r_2}{r_1}) \\\ \Rightarrow {V_b} - {V_a} = \dfrac{W}{q} $$ Hence the work done is obtained as $q(V_b - V_a) = \dfrac{q \lambda}{2 \pi \varepsilon _0} ln(\dfrac{r_2}{r_1}) $ . **Note:** The Gauss law is applicable only for the calculation of the electric field in the closed surface area. That is why the cylinder is taken for the purpose of the calculation. The voltage substituted in the work done is the product of the electric field and distance.