Question
Question: A unit vector perpendicular to the plane passing through the points whose position vectors are 2i –...
A unit vector perpendicular to the plane passing through the points whose position vectors are 2i – j + 5k, 4i + 2j + 2k and 2i + 4j + 4k is-
A
626i+j+5k
B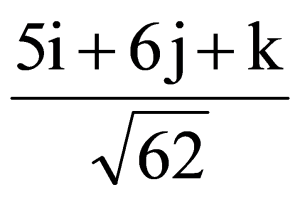
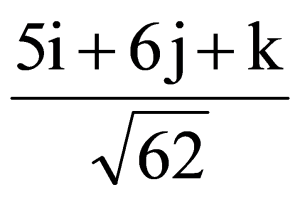
C
62−6i+j+5k
D
1079i+j−5k
Answer
626i+j+5k
Explanation
Solution
If A, B, C are the three points
AB = 2i + 3j – 3k, AC= 5j – k
Required unit vector = ∣AB×AC∣AB×AC = 626i+j+5k
