Solveeit Logo
Login

Question

Question: A unit radian is approximately equal to [a] \(57{}^\circ 17'43''\) [b] \(57{}^\circ 17'45''\) ...

A unit radian is approximately equal to
[a] 57∘17′43′′57{}^\circ 17'43''
[b] 57∘17′45′′57{}^\circ 17'45''
[c] 57∘17′47′′57{}^\circ 17'47''
[d] 57∘17′49′′57{}^\circ 17'49''

Explanation

Solution

Hint: Use the fact that one complete angle in degrees is equal to 360∘360{}^\circ and in radians is equal to 2π2\pi radians. Hence find the measure of one radian in degrees.

Complete step-by-step answer:
Systems of measurement of an angle:
[i] Sexagesimal system or English system: In this system of measurement, an angle is measured in degrees, minutes and seconds. One complete rotation is equal to 360∘360{}^\circ , and one degree consists of 60 minutes and one minute consists of 60 seconds.
[ii] Centesimal system or the French system: In this system of measurement, an angle is measured in grades, minutes and seconds. One right angle consists of 100 grads, and one grade consists of 100 minutes and one minute consists of 100 seconds.
[iii] Circular system: This is the standard system of measurement of an angle. In this system, an angle is measured in radians. The angle subtended by an arc of length equal to the radius of a circle at the centre of the circle is equal to 1 radian.

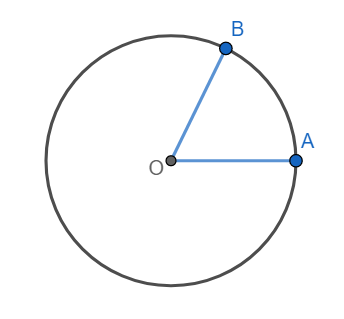
Consider angle AOB in which OA = 1unit and arc AB is of length 1 unit. Hence according to the definition ∠AOB=1\angle AOB=1 radians.
Since the complete length of the circular arc =2π=2\pi , we have one complete rotation that is equal to 2π2\pi radians.
But one complete rotation is equal to 360∘360{}^\circ
Hence we have
360∘=2π360{}^\circ =2\pi radians
Hence 1 radian = 360∘2π=57.296∘1\text{ radian = }\dfrac{360{}^\circ }{2\pi }=57.296{}^\circ
Now we have 0.296∘=0.296×60=17.76′0.296{}^\circ =0.296\times 60=17.76'
Also, we have 0.76′=0.76×60=45.6′′0.76'=0.76\times 60=45.6''
Hence 1 radian ≈57∘17 !!′!! 45′′1\text{ radian }\approx \text{57}{}^\circ \text{17 }\\!\\!'\\!\\!\text{ 45}''
Hence option [b] is correct.

Note: Alternatively, we can find the measure of one radian by calculating the area of the sector AOB in two different ways.
In the circulatory system area of the sector AOB =12π×π(1)2=\dfrac{1}{2\pi }\times \pi {{\left( 1 \right)}^{2}}
In the sexagesimal system area of sector AOB =θ360∘×π(1)2=\dfrac{\theta }{360{}^\circ }\times \pi {{\left( 1 \right)}^{2}}, where θ\theta is the measure of the angle in the sexagesimal system.
Hence we have
θ360∘×π=12π×π ⇒θ=360∘2π \begin{aligned} & \dfrac{\theta }{360{}^\circ }\times \pi =\dfrac{1}{2\pi }\times \pi \\\ & \Rightarrow \theta =\dfrac{360{}^\circ }{2\pi } \\\ \end{aligned}
which is the same as obtained above.