Question

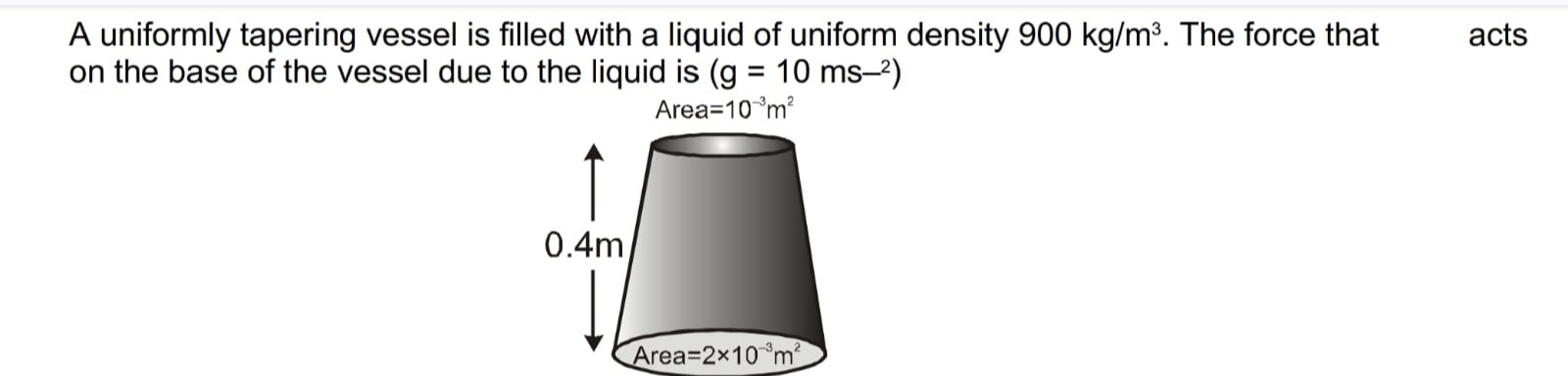
A uniformly tapering vessel is filled with a liquid of uniform density 900 kg/m³. The force that acts on the base of the vessel due to the liquid is (g = 10 ms⁻²)

Area=$10^{-3}m^2$ 0. 4m Area=$2 \times 10^{-3}m^2$

• A. 7.2 N
• B. 3.6 N
• C. 14.4 N
• D. 18 N

Answer 1

Answer: (A)

7.2 N

Answer 2

The force acting on the base of the vessel due to the liquid is the hydrostatic force. This force is calculated as the product of the pressure at the base and the area of the base. The pressure at the base of the liquid column is given by the hydrostatic pressure formula: $P = \rho g h$ where $\rho$ is the density of the liquid, $g$ is the acceleration due to gravity, and $h$ is the height of the liquid column.

The force on the base ($F_{base}$) is then: $F_{base} = P \times A_{base}$ Substituting the expression for pressure: $F_{base} = (\rho g h) \times A_{base}$

Given values: Density of the liquid, $\rho = 900$ kg/m³ Height of the liquid, $h = 0.4$ m Acceleration due to gravity, $g = 10$ m/s² Area of the base, $A_{base} = 2 \times 10^{-3}$ m²

Calculating the pressure at the base: $P = (900 \text{ kg/m³}) \times (10 \text{ m/s²}) \times (0.4 \text{ m})$ $P = 3600 \text{ N/m²}$ (Pascals)

Calculating the force on the base: $F_{base} = (3600 \text{ N/m²}) \times (2 \times 10^{-3} \text{ m²})$ $F_{base} = 7.2 \text{ N}$