Question

A uniformly tapering conical wire is made from a material of Young's modulus $\gamma$ and has a normal, unextended length ${\text{L}}$. The radii, at the upper and lower ends of this conical wire, have values ${\text{R}}$ and ${\text{3R}}$, respectively. The upper end of the wire is fixed to a rigid support and a mass ${\text{M}}$ is suspended from its lower end. The equilibrium extended length, of this wire, would equal to:

(A). ${\text{L}}\left( {1 + \dfrac{1}{3}\dfrac{{{\text{Mg}}}}{{\pi \gamma {{\text{R}}^2}}}} \right)$
(B). ${\text{L}}\left( {1 + \dfrac{2}{9}\dfrac{{{\text{Mg}}}}{{\pi \gamma {{\text{R}}^2}}}} \right)$
(C). ${\text{L}}\left( {1 + \dfrac{1}{9}\dfrac{{{\text{Mg}}}}{{\pi \gamma {{\text{R}}^2}}}} \right)$
(D). ${\text{L}}\left( {1 + \dfrac{2}{3}\dfrac{{{\text{Mg}}}}{{\pi \gamma {{\text{R}}^2}}}} \right)$

Answer 1

- Hint: Formula for the extensions are only applied to the objects having uniform cross-sectional area, but here the cross-sectional area is changing along the length. But we know that by performing the integration of the small cut portion of the object and then applying the limits we will get the value of extension for the whole object.

Complete step-by-step answer:
Let us assume that at the distance ${\text{x}}$ from the bottom end, there is a disc of uniform cross-section, and this is having length ${\text{dx}}$ , and the whole wire is made up of such disc whose radius is increasing gradually. So, we will calculate the change in length of this small portion and after that we will perform integration and then we will get to know the change in the length.

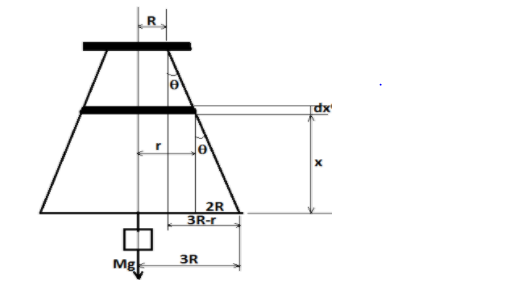
According to the diagram we can write the value of $\tan \theta$ in two ways, as follows
$\tan \theta {\text{ = }}\dfrac{{3{\text{R - r}}}}{{\text{x}}}$ -------equation (1)
Also,
$\tan \theta {\text{ = }}\dfrac{{3{\text{R - R}}}}{{\text{L}}} = \dfrac{{{\text{2R}}}}{{\text{L}}}$ ----equation (2)
Now equating equation (1) and (2)
$\dfrac{{2{\text{R}}}}{{\text{L}}} = \dfrac{{3{\text{R - r}}}}{{\text{x}}}$
$\Rightarrow \dfrac{{2{\text{Rx}}}}{{\text{L}}} = 3{\text{R - r}}$
${\text{r = 3R - }}\dfrac{{2{\text{Rx}}}}{{\text{L}}}$ -----equation (3)
So, this is the value of the radius of the disc at any general position.
Now we will find the extension in the small disc where force is ${\text{Mg}}$ and length ${\text{dx}}$ and area $\pi {r^2}$,
So, the extension in that small disc is as follows,
${(\Delta {\text{l)}}_{{\text{dx}}}}{\text{ = }}\dfrac{{{\text{Mg}} \times {\text{dx}}}}{{\pi {r^2} \times \gamma }}$
Now if we have to calculate the extension in the whole wire which is having increasing cross- sectional area then we have to integrate this extension for the whole length,
${(\Delta {\text{l)}}_{total}} = \int\limits_0^{\text{L}} {{{(\Delta {\text{l)}}}_{{\text{dx}}}}} = \int\limits_0^{\text{L}} {\dfrac{{{\text{Mg}} \times {\text{dx}}}}{{\pi {r^2} \times \gamma }}}$
$\Rightarrow {(\Delta {\text{l)}}_{{\text{total}}}}{\text{ = }}\dfrac{{{\text{Mg}}}}{{\pi \gamma }}\int\limits_0^{\text{L}} {\dfrac{{{\text{dx}}}}{{{r^2}}}}$
$\Rightarrow {(\Delta {\text{l)}}_{{\text{total}}}}{\text{ = }}\dfrac{{{\text{Mg}}}}{{\pi \gamma }}\int\limits_0^{\text{L}} {\dfrac{{{\text{dx}}}}{{{{\left( {3{\text{R - }}\dfrac{{2{\text{Rx}}}}{{\text{L}}}} \right)}^2}}}}$ , putting the value of the ${\text{r}}$ from equation (3)
$\Rightarrow {(\Delta {\text{l)}}_{{\text{total}}}}{\text{ = }}\dfrac{{{\text{Mg}}}}{{\pi \gamma }}\left[ {\dfrac{{ - 1}}{{\left( {{\text{3R - }}\dfrac{{2{\text{Rx}}}}{{\text{L}}}} \right)}} \times \dfrac{1}{{\dfrac{{ - 2{\text{R}}}}{{\text{L}}}}}} \right]_0^{\text{L}}$
$\Rightarrow {(\Delta {\text{l)}}_{{\text{total}}}}{\text{ = }}\dfrac{{{\text{MgL}}}}{{2\pi \gamma {\text{R}}}}\left[ {\dfrac{1}{{\left( {{\text{3R - }}\dfrac{{2{\text{Rx}}}}{{\text{L}}}} \right)}}} \right]_0^{\text{L}}$
$\Rightarrow {(\Delta {\text{l)}}_{{\text{total}}}}{\text{ = }}\dfrac{{{\text{MgL}}}}{{2\pi \gamma {\text{R}}}}\left[ {\dfrac{1}{{\text{R}}} - \dfrac{1}{{3{\text{R}}}}} \right] = \dfrac{{{\text{MgL}}}}{{2\pi \gamma {\text{R}}}} \times \dfrac{2}{{3{\text{R}}}}$
$\Rightarrow {(\Delta {\text{l)}}_{{\text{total}}}}{\text{ = }}\dfrac{{{\text{MgL}}}}{{3\pi \gamma {{\text{R}}^2}}}$
This the total extension in the tapered wire.
So now to get the equilibrium extended length of the wire, we have to add the total length of the wire (without extension)
So ${{\text{L}}_{total}} = {\text{L + }}{\left( {\Delta {\text{l}}} \right)_{total}}$
$\Rightarrow {{\text{L}}_{total}} = {\text{L + }}\dfrac{{{\text{MgL}}}}{{3\pi \gamma {{\text{R}}^2}}}$
${{\text{L}}_{total}} = {\text{L}}\left( {{\text{1 + }}\dfrac{1}{3}\dfrac{{{\text{Mg}}}}{{\pi \gamma {{\text{R}}^2}}}} \right)$
Hence option (A) is the correct answer.

Note: In the solution of the above question there is a use of young’s modulus. Young’s modulus is a measurement of the stiffness or resistance to elastic deformation under load. It also relates the stress and strain acting on any object. Young’s modulus is equal to the stress divided by the strain. The SI Unit for the young’s modulus is ${N/m^{2}}$ .