Question
Question: A uniformly charged thin spherical shell of radius \[\] carries uniform surface charge density of \(...
A uniformly charged thin spherical shell of radius $$$$ carries uniform surface charge density of σ per unit area. It is made of two hemispherical shells, held together by pressing them with force F (see figure). F is proportional to:
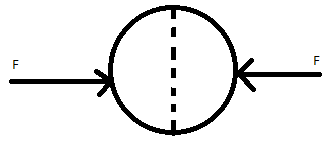
A. ε∘1σ2R2
B. ε∘1σ2R
C. ε∘1Rσ2
D. ε∘1R2σ2
Solution
First let us see what pressure is:
The amount of force exerted per area is known as pressure.
So, force = pressure × area
We have to use this relation in this solution to find the force.
Complete step by step solution:
Now let us find the electrostatic pressure on the surface of a charged conductor-
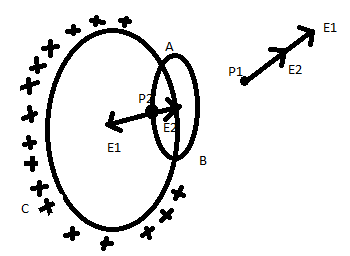
On its surface, the charge given to a conductor is evenly distributed. A repulsive force acts on the conductor through the charge on the rest part of the charge present on the conductor at the small element, and hence, a repulsive force acts on the conductor at each small element, and the overall force on the conductor’s surface is the amount of force vector acting on all the small elements.
It is why the charged conductor has pressure on the charged conducting surface outside.
Let the density of surface charge on the conductor’s surface be σ . The points outside and within the conductor, be labelled as points P1 and P2 respectively.
The electric field outside the charged conducting surface is ε∘σ .
Thus, electric field at point P1 is
EP1=ε∘σ ...... (i)
Electric field inside the conductor is zero. Thus, electric field at P2 is-
EP2=0 ...... (ii)
Now, we divide the conductor into two parts:
a. Element AB whose surface is ds
b. The remaining part ACB
Let the electric field intensity near element AB be E1 and in the part ACB be E2
EP1=E1+E2 ...... (iii)
( E1 and E2 are in the same direction at P1 )
EP2=E1−E2 ...... (iv)
( E1 and E2 are in the opposite direction at P2 )
From equations (2) and (4), we get-
E1−E2=0
E1=E2 ...... (v)
From equations (i), (iii) and (v), we get-
E2=2ε∘σ
We take this as the pressure,
P=2ε∘σ
Hence, force = pressure × area
=2ε∘σ×πR2
If we take 2π as the constant, then
Force αε∘1σ2R2
Hence, option A is the answer.
Note:
Here we have to remember or establish the relationship for pressure. Only then we will be able to find the force for the given question.
