Question
Question: A uniformly charged rod of length 4cm and linear charge density \[\lambda = 30{\rm{ }}\mu {{\rm{C}} ...
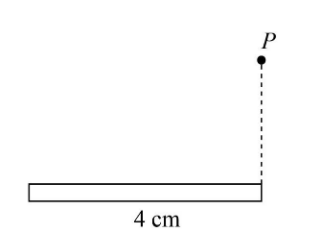
A uniformly charged rod of length 4cm and linear charge density λ=30μC/Cmm is placed as shown in figure. Calculate the x-component of electric field at point P
Solution
We will use the expression for electric field in x-direction of the rod which gives us the relation between linear charge density, vertical distance between point P and rod, Coulomb’s constant and angles made by electric field with the vertical.
Complete step by step answer:
Given:
The length of rod is l=4cm×(100cmm)=0.04m.
The distance between rod and point P is r=3cm=3cm×(100cmm)=0.03m.
The linear charge density is λ=30μC/Cmm.
We have to calculate the x-component of electric point P.
Let us write the general expression for the electric field in the x-direction of rod.
Ex=rkλ(cosθ1−cosθ2)……(1)
Here k is the Coulomb’s constant for air, θ1 is the angle at point P and
θ2 is the angle at another point Q if it exists in negative y-direction in a similar fashion as that of P.
We know that the value of Coulomb’s constant is given as:
\tan \theta = \left( {\dfrac{{{\rm{4 cm}}}}{{3{\rm{ cm}}}}} \right)\\
= \dfrac{4}{3}
\theta = {\tan ^{ - 1}}\left( {\dfrac{4}{3}} \right)\\
= 53.13^\circ
{E_x} = \dfrac{{\left( {9 \times {{10}^9}{\rm{ N}} \cdot {{{{\rm{m}}^2}} {\left/
{\vphantom {{{{\rm{m}}^2}} {{{\rm{C}}^2}}}} \right.
} {{{\rm{C}}^2}}}} \right)\left( {30{\rm{ }}\mu {{\rm{C}} {\left/
{\vphantom {{\rm{C}} {\rm{m}}}} \right.
} {\rm{m}}}} \right)}}{{0.03{\rm{ m}}}}\left( {\cos 53.13^\circ - \cos 0^\circ } \right)\\
= \dfrac{{\left( {9 \times {{10}^9}{\rm{ N}} \cdot {{{{\rm{m}}^2}} {\left/
{\vphantom {{{{\rm{m}}^2}} {{{\rm{C}}^2}}}} \right.
} {{{\rm{C}}^2}}}} \right)\left( {30 \times {{10}^{ - 6}}{{\rm{C}} {\left/
{\vphantom {{\rm{C}} {\rm{m}}}} \right.
} {\rm{m}}}} \right)}}{{0.03{\rm{ m}}}}\left( {\cos 53.13^\circ - \cos 0^\circ } \right)\\
= - 36 \times {10^5}{\rm{ }}{{\rm{N}} {\left/
{\vphantom {{\rm{N}} {\rm{C}}}} \right.
} {\rm{C}}}
