Question

A uniformly charged and infinitely long line having a linear charge density is placed at a normal distance y from a point O. Consider a sphere of radius R with O as the center and R>y. Electric flux through the surface of the sphere is :

A. Zero
B. $\dfrac{2\lambda R}{{{\epsilon }_{0}}}$
C. $\dfrac{2\lambda \sqrt{{{R}^{2}}-{{y}^{2}}}}{{{\epsilon }_{0}}}$
D. $\dfrac{\lambda \sqrt{{{R}^{2}}-{{y}^{2}}}}{{{\epsilon }_{0}}}$

Answer 1

Here, the charge on the system is only due to the long infinite wire as the sphere is neutral and hence possesses no other charge. We will find the charge enclosed in the sphere by using the linear charge density and calculate the length of the wire which is inside the sphere and apply Gauss’ law to obtain the electric flux.

Complete step by step answer:

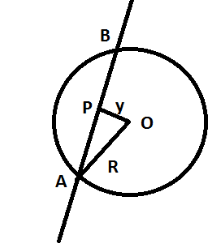
Here, the length between O and P is y, while OA is the radius of the circle which is denoted by R. Also, AB is the part of the wire which is passing through the sphere; hence AB is the diameter of the sphere. Now, the long infinite wire has a charge density on it, while the sphere is neutral.The linear charge density on the long infinite wire is. Now, the triangle OAP forms a Pythagorean triangle, which is a right angled triangle. Thus, we can find the distance AP, such that:

$$A{P^2} = {R^2} - {y^2} \\\ \Rightarrow AP = \sqrt {{R^2} - {y^2}} \\\$$

Now, AP is only the half of the distance covered by the wire inside the sphere. Thus, the charge enclosed inside the sphere due to the wire is:
Now, from Gauss's law, we know that the electric flux through any surface is given by the ratio of the charge enclosed inside the surface and the electric permittivity. Here,$\phi$ is the electric flux and $Q$ is the charge enclosed and is the permittivity of the material. Thus,

\therefore\phi =\dfrac{2\lambda \centerdot \sqrt{{{R}^{2}}-{{y}^{2}}}}{{{\epsilon }_{0}}}$$ **Hence, option C is the correct answer.** **Note:** From the relation of the electric flux, we can observe that the more the distance of the wire is from the center of the sphere, the lesser would the electric flux of the sphere will be as the length of the wire passing through the sphere will decrease, while the maximum electric flux will be obtained when the wire passes through the center of the sphere.