Question

A uniform wooden stick of mass $1.6\ kg$ and length l rests in an inclined manner on a smooth, vertical wall of height h < l such that a small portion of the stick extends beyond the wall. The reaction force of the wall on the stick is perpendicular to the stick. The stick makes an angle of ${{30}^{\circ }}$ with the wall and the bottom of the stick is on a rough floor. The reaction of the wall on the stick is equal in magnitude to the reaction of the floor on the stick. The ratio of $h/l$ and the frictional force $f$ at the bottom of the stick are $\left( g=10\ m/{{s}^{2}} \right)$:

(a) $\dfrac{h}{l}=\dfrac{\sqrt{3}}{16},f=\dfrac{16\sqrt{3}}{3}N$
(b) $\dfrac{h}{l}=\dfrac{3}{16},f=\dfrac{16\sqrt{3}}{3}N$
(c) $\dfrac{h}{l}=\dfrac{3\sqrt{3}}{16},f=\dfrac{8\sqrt{3}}{3}N$
(d) $\dfrac{h}{l}=\dfrac{3\sqrt{3}}{16},f=\dfrac{16\sqrt{3}}{3}N$

Answer 1

Hint: First of all, we will resolve all the forces acting on the wooden stick due to the sides of the wall, then we will find the components of the forces with respect to the x and y axis. Then using newton’s law i.e. summation of forces should be zero if body is in equilibrium which can be given as $\sum{{{F}_{\left( x,y \right)}}}=0$, we will find the values of frictional force. Then the torque acting should also be zero as the body has to remain in equilibrium so, using the torque balance equation i.e. ${{\tau }_{net}}=0$, we will find the ratio of height and length.
Formula used: $\sum{{{F}_{\left( x,y \right)}}}=0$, ${{\tau }_{net}}=0$

Complete step by step answer: In question we are given that a wooden stick of mass $1.6kg$ and length l is resting in a vertical manner on a smooth wall. Now, due to that the reaction force of the wall acts on the stick. Now, the stick is making an angle of ${{30}^{\circ }}$ with the wall and its bottom rests on a rough floor, so due to sliding the stick sliding force acts on the stick opposite to the direction of sliding of the stick. And we are asked to find the ratio of $\dfrac{h}{l}$ and frictional force $f$. So, first of all we will draw a diagram based on the given data for our simplicity.

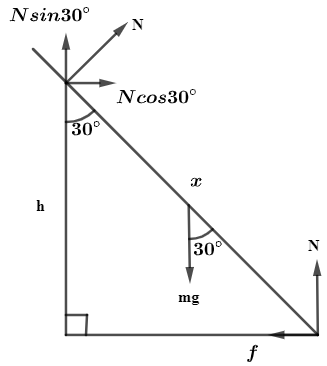
Now, from figure it can be said that at point A, a reaction force acts on the stick due to the wall in the direction opposite to the direction of force acting on the wall due to the stick. In the same way, the reaction force also acts on point B, and weight of the stick is shown downwards.

Now, considering the reaction force at point A, we will divide the force in x and y as shown in the figure and in the same way we will divide the components of force at point B.

Now, in question it is given that the system is in equilibrium, and we know that when system is in equilibrium the net force acting on the body is zero, which can be shown mathematically as,

$\sum{{{F}_{\left( x,y \right)}}}=0$
Considering the vertical components i.e. $\sum{{{F}_{y}}}=0$can be given as,
$\Rightarrow N+N\sin 30-mg=0$
$\Rightarrow N+N\sin 30=mg$
$\Rightarrow N\left( 1+\sin 30 \right)=mg$
we know that $\sin 30=\dfrac{1}{2}$, so substituting it in the expression above we will get,
$\Rightarrow N\left( 1+\dfrac{1}{2} \right)=mg$
$\Rightarrow N=\dfrac{2mg}{3}$………………..(i)

Now, considering the horizontal components i.e. $\sum{{{F}_{x}}}=0$can be given as,
$N\cos 30-f=0$
$\Rightarrow N\cos 30=f$
Now, we know that $\cos 30=\dfrac{\sqrt{3}}{2}$, so substituting it in the expression above we will get,
$\Rightarrow N\dfrac{\sqrt{3}}{2}=f$ …………………(ii)

Now, substituting the value of N from expression (i) in expression (ii) we will get,
$\Rightarrow \left( \dfrac{2mg}{3} \right)\dfrac{\sqrt{3}}{2}=f$
$m=1.6$, $g=10$is given in the question, so on substituting them we will get,
$\Rightarrow \left( \dfrac{2\left( 1.6 \right)\left( 10 \right)}{3} \right)\dfrac{\sqrt{3}}{2}=f$
$\Rightarrow f=\left( \dfrac{16\sqrt{3}}{3} \right)N$
Now, the torque acting on the stick due to reaction forces should also be zero as the body has to remain in equilibrium so, it can be given mathematically as,
${{\tau }_{net}}=0$
$\Rightarrow N\times x=mg\times \dfrac{l}{2}\sin 30$
$\Rightarrow N\times x=mg\times \dfrac{l}{2}\sin 30$

Substituting the value of N from expression (i) we will get,

$\Rightarrow \left( \dfrac{2mg}{3} \right)\times x=mg\times \dfrac{l}{2}\sin 30$
$\Rightarrow x=mg\times \dfrac{l}{2}\times \dfrac{1}{2}\times \dfrac{3}{2mg}=\dfrac{3l}{8}$
Now, considering the right-angle triangle formed in the figure, side h can be obtained by considering x as hypotenuse, this can be seen mathematically as,
$\cos 30=\dfrac{h}{x}\Rightarrow h=x\cos 30$

On substituting the value of x we will get,

$\cos 30=\dfrac{h}{x}\Rightarrow h=\dfrac{3l}{8}\dfrac{\sqrt{3}}{2}$
$\dfrac{h}{l}=\dfrac{3\sqrt{3}}{16}$.
Thus, the ratio of $\dfrac{h}{l}$ is $\dfrac{3\sqrt{3}}{16}$ and value of frictional force is $\left( \dfrac{16\sqrt{3}}{3} \right)N$.
Hence, option (d) is the correct answer.

Note: Students might make mistakes in considering the vertical and horizontal components and may also make mistakes in considering the directions of the force acting. So, to avoid that students must adopt a basic method to consider the direction of force acting such as, the mg always acts downwards and one can consider the forces acting upward as positive and downward as negative for vertical and forces acting in right direction as positive and acting in left direction as negative for horizontal. By doing so, the students won’t get confused and maximum errors can be taken care of.