Question

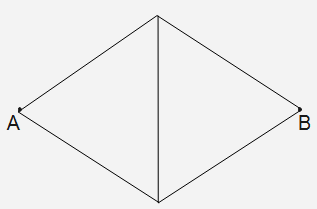
A uniform wire of resistance R is stretched n times and then cut to form 5 identical wires. These wires are arranged as shown in the figure. Find the effective resistance between A and B.

Answer 1

In this question, we will use the direct formula which gives relation between resistance, resistivity, area and length of a wire. Further, by substituting and solving for effective resistance of new wire, we will get the required result. We will also study the basics of a simple circuit, for our better understanding.

Formula used:
$R = \dfrac{{\rho l}}{A}$

Complete step by step solution:
We know that the electrical resistance of a circuit or device is defined as the ratio of the applied voltage V to the current I which flows through it.
$R = \dfrac{{\rho l}}{A}$
We are given that:
$Al = const.$
So, the new cross sectional area of the wire will be:
\eqalign{ & \Rightarrow A'nl = Al \cr & \Rightarrow A' = A/n \cr}
Now, the resistance offered by the new wire will be given by:
$R' = \dfrac{{\rho (nl)}}{{A'}}$
Now, by putting the value of A’ in above equation, we get:
$R' = \dfrac{{\rho (nl)}}{{A/n}}$
$R' = {n^2}\left( {\dfrac{{\rho l}}{A}} \right)$
$\Rightarrow R' = {n^2}R$
Now, since the wire is cut into 5 parts, the above equation becomes:
$E{'_r} = \dfrac{{R'}}{5} = \dfrac{{{n^2}R}}{5}$
Therefore, the required effective resistance of the given wire is represented by the above result.

Additional information:
We should know that in a series circuit, the output current of the first resistor flows into the input of the second resistor; so, the current is the same in each resistor whereas In a parallel circuit, all of the resistor are on connected together on one side and all the leads on the other side are connected together.
In a circuit if the resistance is constant over a range of voltage, then I = V/R, can be used to predict the behavior of the material. This involves DC current and voltage, it is the same for the resistors. Further, a material obeys Ohm's law or does not obey; the resistance of the material can be described in terms of its bulk. The resistivity, and the resistance both, is temperature dependent. Over certain ranges of temperature, this temperature dependence can be predicted from resistance.

Note:
In series connection the resistances are directly added whereas in parallel connection resistance is added inversely. Internal resistance of a circuit refers to the opposition to the flow of current offered by the cells and batteries themselves thereby, resulting in the generation of heat. Internal resistance and resistance both are measured in Ohms.