Question

A uniform wire of resistance $24\Omega$ is used to form a regular hexagon $ABCDEFA$ . The equivalent resistance of the loop between $A$ and $B$ is $..........\Omega$
$\left( A \right){\text{ 4}}{\text{.8}}\Omega$
$\left( B \right){\text{ 3}}{\text{.3}}\Omega$
$\left( C \right){\text{ 48}}\Omega$
$\left( D \right){\text{ 33}}\Omega$

Answer 1

Since we have a regular hexagonal structure so between $A$ and $B$ it will be in parallel resistance. So by using the parallel formula for the resistance, we will be able to solve this question and get to the exact answer.

Formula used
When resistance is in parallel, then
$\dfrac{1}{{{R_T}}} = \dfrac{1}{{{R_1}}} + \dfrac{1}{{{R_2}}} + \dfrac{1}{{{R_3}}} + ...$
Here, ${R_T}$ will be the equivalent resistance
And ${R_1},{R_2},{R_3}$ will be the resistance connected to it in parallel.

Complete step by step solution

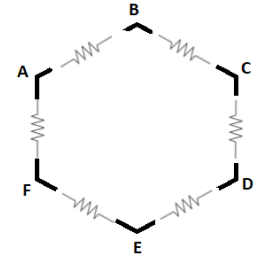
Since the wire is $24\Omega$ so by doubling it back on itself. Then it will be divided into six parts and leaving $4\Omega$ per segment.
Therefore from this, we will get a resistance of $20\Omega$ and $4\Omega$ . So by using the formula of resistance in parallel, we will get the equivalent resistance as
$\Rightarrow {R_T} = \dfrac{{{R_A}{R_B}}}{{{R_A} + {R_B}}}$
Now on substituting the values, we will get
$\Rightarrow {R_T} = \dfrac{{4 \times 20}}{{4 + 20}}$
And solving the above expression, we get
$\Rightarrow {R_T} = \dfrac{{80}}{{24}}$
And on solving the division, we will get the equation as
$\Rightarrow {R_T} = 3.33\Omega$
Therefore, the equivalent resistance of the loop between $A$ and $B$ is $3.33\Omega$ .
Hence, the option $\left( b \right)$ is correct.

Additional information
In a parallel circuit, the total current will be equal to the sum of the current in the single circuit whereas in a series circuit, in each of the circuits the current will be similar. In the parallel circuit the voltage across the resistor will be equal to the supply voltage whereas, in a series circuit, the total voltage drop will be the same as the supply voltage.

Note
In a parallel circuit the effective resistance will be more than the minimum value resistance but in parallel, the effective resistance is always less than the minimum value resistance. From this point we can also check if the answer we got is correct or not.