Question

A uniform wire of resistance $20\Omega$ having resistance $1\Omega {{m}^{-1}}$ is bent in the form of a circle as shown in fig. If the equivalent resistance between M and N is $1.8\Omega$ ,then the length of the shorter section is:

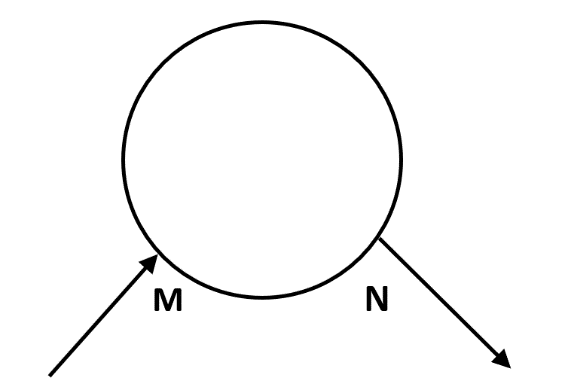
$\begin{aligned} & (a)2m \\\ & (b)5m \\\ & (c)1.8m \\\ & (d)18m \\\ \end{aligned}$

Answer 1

Since it has been given to us that the current enters through M and exits through N. We can say that the shorter part of the circle and the bigger part of the circle are in parallel to each other as they are connected to the same points across both the terminal and are under the same potential difference too.

Complete step-by-step answer:
It has been given to us that the net resistance of the wire frame (say R) is $20\Omega$ . Also, its resistance per unit length (say r) is given to be $1\Omega$ per meter. Hence, the total length (say L) of the wire frame can be calculated as:
$\begin{aligned} & \Rightarrow L=\dfrac{20}{1}m \\\ & \Rightarrow L=20m \\\ \end{aligned}$
Now, let the length of the shorter section of the wire frame be $(x)$meter, then the length of the larger section of the wire frame will be equal to $(20-x)m$ .
Then, the resistance of the shorter wire frame (say ${{r}_{1}}$ ) will be equal to $(x)\Omega$ and the resistance of the larger wire (say ${{r}_{2}}$ ) frame will be equal to $(20-x)\Omega$ .
Since the two sections of wire are connected in parallel, their net resistance can be given by the formula:
$\Rightarrow {{r}_{net}}=\dfrac{{{r}_{1}}{{r}_{2}}}{{{r}_{1}}+{{r}_{2}}}$
Here, the value of net resistance is given in the problem and its value is $1.8\Omega$ .
Thus, putting this value in the above equation, we get:
$\begin{aligned} & \Rightarrow 1.8=\dfrac{x(20-x)}{x+(20-x)} \\\ & \Rightarrow 1.8=\dfrac{x(20-x)}{20} \\\ & \Rightarrow 36=20x-{{x}^{2}} \\\ \end{aligned}$
On rearranging terms, we get:
$\begin{aligned} & \Rightarrow {{x}^{2}}-20x+36=0 \\\ & \Rightarrow (x-2)(x-18)=0 \\\ & \Rightarrow x=2;18 \\\ \end{aligned}$
Here, we get two values of $(x)$ that are $x=2$ and $x=18.$
Since, we assumed $(x)$ to be the shorter distance, hence $x=2$is the acceptable value.
Hence, the length of the shorter section between the points M and N is 2m.

So, the correct answer is “Option A”.

Note: Even though the problem has a circuit in the form of a loop or some irregular shape, we should be able to analyze the given electrical circuit properly. Once, we do that what’s left of the problem is simple mathematical calculation and nothing else.