Question

A uniform wire of $16\Omega$ resistance is made into the form of a square. Two opposite corners of the square are connected by a wire of resistance $16\Omega$. The effective resistance between the other two opposite corner is
(A) $32\Omega$
(B) $16\Omega$
(C) $8\Omega$
(D) $4\Omega$

Answer 1

Hint The configuration of the wires is similar to that of a Wheatstone bridge. The voltage between the two parallel resistors of a Wheatstone bridge is zero if it is balanced. So on removing the middle wire, we can then calculate the equivalent resistance.
In this solution we will be using the following formula;
$\Rightarrow \dfrac{1}{{{R_{eq}}}} = \dfrac{1}{{{R_1}}} + \dfrac{1}{{{R_2}}} + ... + \dfrac{1}{{{R_n}}}$ where ${R_{eq}}$ is the equivalent resistance of a resistors in parallel, ${R_1}....{R_n}$ are the individual resistors in the parallel configuration.
$\Rightarrow {R_{eqs}} = {R_1} + {R_2} + ... + {R_n}$where${R_{eqs}}$ is the equivalent resistance of resistors in series and ${R_1}....{R_n}$ are the individual resistances.

Complete step by step answer

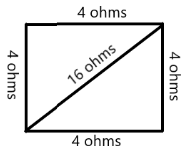
The figure above shows the wire after it has been made into a square with the sixteen ohms resistor connected across the two corners of the square. This configuration resembles a Wheatstone bridge as shown in the figure below in a more familiar setting

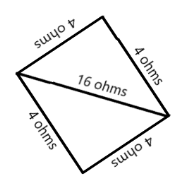
To calculate the equivalent resistance, we assume a voltage is applied at any of the opposite corners of the square. This is allowed because all resistances are equal.
Let’s say we placed the voltage at the opposite corners to where the 16 Ohms resistor is connected. Since, it is a balanced Wheatstone bridge, the voltage across the 16 Ohms is zero. Hence, we can ignore the 16 Ohms resistance. The two resistance at the top are in series, likewise the two at the bottom. Hence,
For top resistance
$\Rightarrow {R_{eq1}} = {R_1} + {R_2} = 4 + 4 = 8\Omega$
For bottom resistance, similarly,
$\Rightarrow {R_{eq2}} = 4 + 4 = 8\Omega$,
This two resistance are in parallel, and hence calculated as
$\Rightarrow \dfrac{1}{{{R_{eq}}}} = \dfrac{1}{{{R_{eq1}}}} + \dfrac{1}{{{R_{eq2}}}} = \dfrac{1}{8} + \dfrac{1}{8}$
Computing we have that
$\Rightarrow \dfrac{1}{{{R_{eq}}}} = \dfrac{1}{4}$
$\Rightarrow {R_{eq}} = 4\Omega$
Hence, the correct option is D.

Note
To avoid confusions, we are allowed to assume a voltage across the opposite corners because from the definition of equivalent resistance of a circuit, it is the one resistance to the current flow in a circuit which can replace all the resistances in the circuit. Since the voltage across 16 Ohms is zero, no current flows through the resistor, and thus does not count to the equivalent resistance.