Question

A uniform wire is cut into two pieces such that 1 piece is twice as long as the other. The 2 pieces are connected in parallel in the left gap of Meter Bridge. When a resistance of $20\Omega$ is connected in the right gap, the neutral point is obtained at a distance of 60 cm from the right end of the wire. Find out the original resistance of wire before it was cut into 2 pieces.

Answer 1

First find the resistance formed by the left side gap length of the meter bridge by using meter bridge gap method where we find the unknown resistance by equating it with the left and right meter length gap by using the formula:
$X\text{ }=\text{ }\dfrac{R\times \text{ }l}{\left( 100-l \right)}$
where X is the unknown resistance, R is the known resistance, l is the known length of the meter bridge gap.

Complete step by step answer:
As given in the question, one of the pieces is twice as long as other as shown in the diagram below:

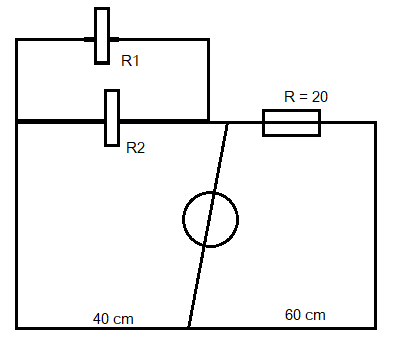
The neutral point from the right is given as 60cm and the distance from the wire is given as 100 cm. Hence, the distance of the wire at the neutral point is x and to find the value of the x, we use the formula of:
$X\text{ }=\text{ }\dfrac{R\times \text{ }l}{\left( 100-l \right)}$
According to the diagram the length of the bridge is 40cm and $R=20\Omega$, we get the value of the unknown resistance X in the left gap as:
$X\text{ }=\text{ }\dfrac{20\times 40}{\left( 100-40 \right)}$
$\Rightarrow X\text{ }=\text{ }\dfrac{20\times 40}{\left( 100-40 \right)}$
$\Rightarrow X\text{ }=\text{ }13.34\Omega$
With the resistance as parallel we will find the value of the resistance by using the formula as:
$\dfrac{1}{{{R}_{1}}}+\dfrac{1}{{{R}_{2}}}=\dfrac{1}{R}$
Now equating the value of the unknown resistance of the meter bridge ${{R}_{X}}$ with the resistance connected in parallel we get the value of:
$\dfrac{{{R}_{1}}{{R}_{2}}\text{ }}{{{R}_{1}}+{{R}_{2}}}=\text{ }\dfrac{l\times {{R}_{X}}}{100-l}$
Placing the value of the parallel resistance as $\dfrac{{{R}_{1}}{{R}_{2}}\text{ }}{{{R}_{1}}+{{R}_{2}}}=13.34\Omega$ and placing the value of length as 40, we get the value of the resistance as:
$\dfrac{40}{60}{{R}_{X}}=13.34\Omega$
${{R}_{X}}=20.04\Omega$
Another piece whose length is double than the other will have the resistance twice as those of the resistance given above as resistance depends upon the length in direct proportionality hence, the two resistances are:
${{R}_{1}}=20.04\Omega$, ${{R}_{2}}=40.04\Omega$. (Resistance 2 is twice that of Resistance 1 due to twice the length of the piece.) Therefore, the original resistance is:
$\therefore 20.04\Omega +40.04\Omega =60.04\Omega$.

Note:
Another method to do the question is to find the resistance first as:
According to the diagram the length of the bridge is 40cm and $R=20\Omega$, we get the value of the unknown resistance X in the left gap as:
$X\text{ }=\text{ }\dfrac{20\times 40}{\left( 100-40 \right)}$
$\Rightarrow X\text{ }=\text{ }\dfrac{20\times 40}{\left( 100-40 \right)}$
$\Rightarrow X\text{ }=\text{ }13.34\Omega$
The total required resistance $R=\dfrac{1}{R1}+\dfrac{1}{R2}$
Use the parallel resistance method to find the total resistance as:
${{R}_{x}}=\dfrac{R1\times R2}{R1+R2}$
With the lengths as $L1+L2=L$ and $L2=2L1$, we get the lengths as $L2=\dfrac{L}{3},L1=\dfrac{2L}{3}$.
With the resistance directly proportional to the length, the resistance $R1,R2$ are $\dfrac{R}{3},\dfrac{2R}{3}$. Placing them in the parallel resistance formula we get:
${{R}_{x}}=\dfrac{\dfrac{R}{3}\times \dfrac{2R}{3}}{\dfrac{R}{3}+\dfrac{2R}{3}}$
${{R}_{x}}=\dfrac{2}{9}R$
Equating the resistance of ${{R}_{x}}$ with $X$, we get the original resistance as:
$\dfrac{2}{9}R=13.34\Omega$
$R=60.04\Omega$