Question
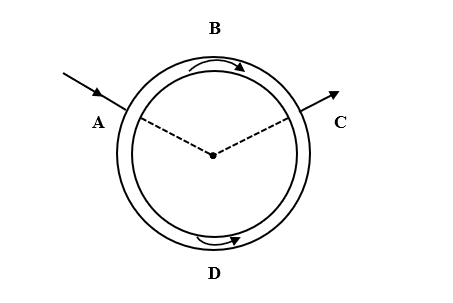
Question: A uniform wire is bent in the form of a circle of radius R. A current I enters at A and leaves at C ...
A uniform wire is bent in the form of a circle of radius R. A current I enters at A and leaves at C as shown in the figure:
If the length ABC is half of the length ADC, the magnitude field at the centre O will be
Solution
To solve this problem, use the Ohm's law to find the potential difference in terms of current and resistance. Then we know, relation between resistance and length of the wire substitute in the equation. Then, using the Biot-Savart's law for magnetic fields inside a wire, find the magnetic field in length ABC and then in length ADC. Substitute the relation obtained above in both the equations. Take the ratio of both the equations and find the relation between magnetic field in length ABC and magnetic field in length ADC.
Formula used:
V=IR
R=ρAl
B=2πR2μ0Ir
Complete answer:
Direction of current in length ABC is opposite to the direction of current in length ADC. Thus, the direction of magnetic fields due to these currents will also be in opposite directions.
According to Ohm’s Law,
V=IR
Where, V is the potential difference
I is the current flowing
R is the resistance
So, applying Ohm’s law across AB we get,
V=i1R1=i2R2 …(1)
We know, formula for resistivity is given by,
R=ρAl
From above equation we can infer that,
R∝l …(2)
Substituting equation. (1) in equation. (2) we get,
V=i1l1=i2l2 …(3)
Now, formula for magnetic field inside a wire given by Biot-Savart’s law is,
B=2πR2μ0Ir
Magnetic field due to length ABC is given by,
B1=2πμ0R2i1l1 …(4)
Similarly, Magnetic field due to length ADC is given by,
B2=2πμ0R2i2l2 …(5)
Dividing equation. (4) by (3) we get,
B2B1=i2l2i1l1
Using equation. (3),
B2B1=1
∴B1=B2
Hence, both the magnetic fields are equal but are opposite in direction.
Thus, the resultant magnetic field at the center O will be zero.
Note:
Students must remember the basic formulas like Biot-Savart's law and Ohm's law to answer these types of questions. Inside the conductor the magnetic field B increases linearly with radius r. Whereas outside the conductor the magnetic field becomes that of a straight conductor and decreases with increase in radius.
