Question

A uniform wire is bent in the form of a circle as shown in the figure. The effective resistance between A and B is maximum if $\theta$ is

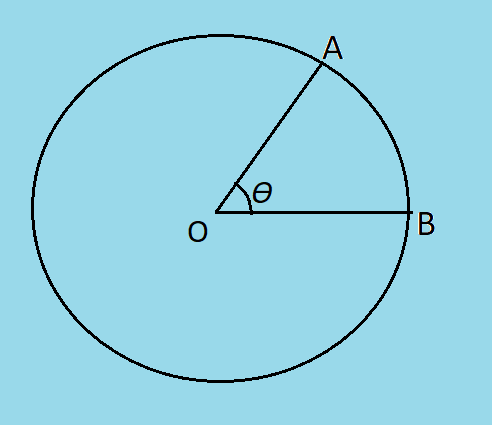
(1) $180^\circ$
(2) $90^\circ$
(3) $45^\circ$
(4) $60^\circ$

Answer 1

The above problem can be solved by using the concept of the resistance. The resistance of the wire is defined as the effect that opposes the flow of the charge in the wire. It varies with the material and geometry of the wire. The increase in the temperature decreases the resistance of the wire.

Complete step by step answer
Given: The angle subtended by the section AB is $\theta$.
Let us assume that the radius of the circle is r and the length of the arc AB is $l$.
The formula to find the length of the arc AB is,
$l = 2\pi r\left( {\dfrac{\theta }{{2\pi }}} \right)$
The formula to find the resistance of the complete circle is,
$R = \dfrac{{\rho l}}{A}.....\left( 1 \right)$
Here, $\rho$ is the resistivity of the wire and A is the cross sectional area of the wire. The resistivity and cross sectional area of the wire remain constant, so the resistance of the large arc and small arc depends on the length of the circumference of the wire.
Substitute the value of the length of the arc in the equation (1).
$R = \left( {\dfrac{\rho }{A}} \right)\left( {2\pi r\left( {\dfrac{\theta }{{2\pi }}} \right)} \right)$
From the above expression it is clear that the effective resistance across A and B is maximum for the angle $180^\circ$.

Thus, the angle for the maximum effective resistance between A and B is $180^\circ$and the option (1) is the correct answer.

Note: The variable A in the expression of the resistance is the cross sectional area, not the surface area. Always remember this fact as this is confusing and may give the wrong calculation. The resistivity of the wire is the material property and varies with the temperature of the wire.