Question

A uniform tube of length $60\;cm$ stands vertically with its lower end dipping into water. First two air column lengths above water are 15 cm and 45 cm, when the tube responds to a vibrating fork of frequency 500 Hz. Find the lowest frequency to which the tube will respond when it is open at both ends.

Answer 1

When the tube is dipped in water, it behaves as a tube with one closed end. In this case, use the relation between the resonant frequency and the speed of sound and the length of the air column to arrive at an expression for the speed of sound, following which you can substitute the given values to find the same. Following this, treating the resonance tube to be open at both ends, which means that the length of the air column is the entire length of the tube, substitute the obtained value of the speed of sound to arrive at the appropriate minimum frequency.

Formula used:
Resonant frequency for tube closed at one end: $f = \dfrac{nv}{4l}$
Resonant frequency for tube open at both ends: $f = \dfrac{nv}{2l}$.

Complete step by step answer:
We know that acoustic resonance is a phenomenon wherein an acoustic system amplifies the sound waves whose frequency matches its own natural frequency of vibration.
A resonance tube with the lower end closed by water surface will have resonances at frequencies
$f = \dfrac{nv}{4l}$, where n is an odd positive integer, v is the speed of sound, and l is the length of the resonant tube. This tube produces only odd harmonics., i.e., at n, n+2, n+4 and so on
A resonance tube with both its ends open will have resonances at frequencies
$f = \dfrac{nv}{2l}$.
The resonance properties of a resonance tube can be understood by considering the behaviour of a sound wave in air, which propagates via the compressions and rarefactions of the molecules of the medium. Within a tube, a standing wave is formed, with the closed end being the displacement node or the point of no vibration, and the subsequent resonant harmonics are situated at the nodes of the standing wave.
Let us now look at this phenomenon in the context of our question.
When the tube is dipped in water, it behaves as a resonant column with one closed end.

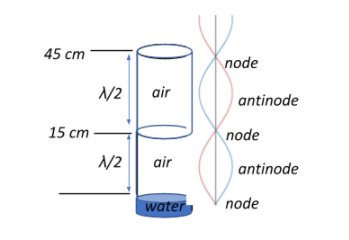
It produces the first harmonic (n=1) at $l=15\;cm =0.15\;m$ and the second harmonic ($n^{\prime}=n+2=1+2=3$) at $l = 45\;cm =0.45\;m$.
$\Rightarrow f_{fork} = \dfrac{1\times v}{4\times 0.15}$ and
$f_{fork}= \dfrac{3 \times v}{4 \times 0.45}$
Solving either equation will give us the speed of sound in air:
Given that $f_{fork} = 500\;Hz$,
$500 = \dfrac{v}{4\times 0.15} \Rightarrow v = 500 \times 4 \times 0.15 = 300\;ms^{-1}$
Now, when the tube is open at both ends, the lowest frequency for which it produces a harmonic (n=1) over the length $l=60\;cm =0.6\;m$ of the resonant tube can be given as:
$f = \dfrac{v}{2l}$
$\Rightarrow f = \dfrac{300}{2 \times 0.6} = 250\;Hz$
Therefore, the lowest frequency to which the tube produces a resonant harmonic is $250\;Hz$.

Note:
Do not forget that the expression for resonances of the resonance tube vary depending on the structure of the tube that we consider, based on whether the tube is open at both ends, or closed at one end, which are given as $\dfrac{nv}{2l}$, where n is any positive integer, and $\dfrac{nv}{4l}$, where n is an odd positive integer, respectively. Subsequent harmonics when the tube is open at both ends are at n =1,2,3.. and so on, whereas subsequent harmonics when the tube is closed at one end are at n = 1,3,5,..and so on. This is because, by definition, closed tubes have a node at one end, and an antinode at the other, so there is no way for even-numbered harmonics to be present.