Question

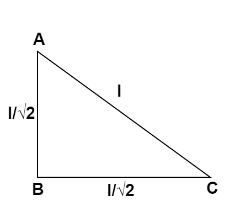
A uniform triangular plate of mass $M$ whose vertices are $ABC$ has lengths $l$ , $\dfrac{l}{{\sqrt 2 }}$ and $\dfrac{l}{{\sqrt 2 }}$ as shown in the figure. Find the moment of inertia of this plate about an axis passing through the point $B$ and perpendicular to the plane of the plate.

Answer 1

Firstly, we will observe the diagram. The sides of the right-angled triangle are given. Then we will find out the moment of inertia of the triangle about the base. We know that the perpendicular axes theorem. We will use this theorem to calculate the moment of inertia along an axis passing through point $B$ .

Complete step by step answer:
Given that the length of $AC$ is $l$ , $AB$ is $\dfrac{l}{{\sqrt 2 }}$ and $BC$ is $\dfrac{l}{{\sqrt 2 }}$ .
Mass of the plate is $M$ .
Moment of inertia of the triangle around the base
$I = \dfrac{{M{h^2}}}{6}$
Therefore the moment of inertia of the specified triangle about base $BC$ .
$\Rightarrow {I_{BC}} = \dfrac{{M{{\left( {\dfrac{1}{{\sqrt 2 }}} \right)}^2}}}{6}$
On further solving the equation we get,
$\Rightarrow {I_{BC}} = \dfrac{{M{l^2}}}{{12}}$
Also the moment of inertia of the triangle about $AB$ .
$\Rightarrow {I_{AB}} = \dfrac{{M{{\left( {\dfrac{l}{{\sqrt 2 }}} \right)}^2}}}{6}$
On further solving the equation we get,
$\Rightarrow {I_{AB}} = \dfrac{{M{l^2}}}{{12}}$
The perpendicular axis theorem states that the moment of inertia of a laminar body around an axis perpendicular to its plane is equal to the sum of the moment of inertia of the laminar around any two mutually perpendicular axes in its plane and intersecting each other at the point wherever the perpendicular axis passes through it.
Using perpendicular axis theorem, we can get,
$\Rightarrow {I_B} = {I_{BC}} + {I_{AB}}$
On substituting all the values in the above equation we get,
${I_B} = \dfrac{{M{l^2}}}{{12}} + \dfrac{{M{l^2}}}{{12}}$
$\Rightarrow {I_B} = \dfrac{{M{l^2}}}{6}$ .

Note:
Moment of inertia is the name given to rotational inertia, and it plays the same role in rotation as is played by mass in translation. The moment of inertia is defined concerning a specific rotation axis. Here we have defined concerning an axis passing through the point $B$ and perpendicular to the plane of the plate.