Question

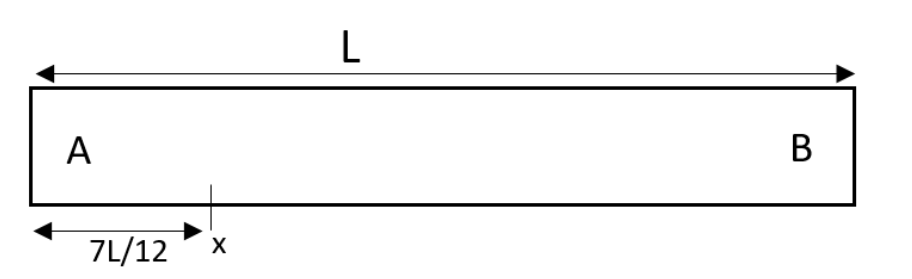
A uniform thin rod AB of length $L$ has linear mass density $\mu \left( x \right)=a+\dfrac{bx}{L}$​, where $x$ is measured from A. If the centre of mass of the rod lies at a distance of $\dfrac{7L}{12}$ from A, then a and b are related as
$\begin{aligned} & A.2a=b \\\ & B.a=2b \\\ & C.a=b \\\ & D.3a=2b \\\ \end{aligned}$

Answer 1

Find out the centre of mass of the rod AB and substitute the terms mentioned in the question in it. Rearrange the equation and reach at the relation between a and b. The centre of mass is the point with respect to a body where the total mass of the body is assumed to be concentrated. This all will help you in answering this question.

Complete step by step answer:
The centre of mass of the rod is to be found. The length of the rod has been mentioned as $L$, the linear mass density has been given by the equation,
$\mu \left( x \right)=a+\dfrac{bx}{L}$
Where $x$ is measured from point A.
The distance of the centre of mass from the point A is given as,
${{x}_{cm}}=\dfrac{7L}{12}$
The centre of mass of the body is given as,
${{x}_{cm}}=\dfrac{\int_{0}^{L}{\mu \left( x \right)xdx}}{\int_{0}^{L}{\mu \left( x \right)dx}}$
Substituting the values in it will give,
${{x}_{cm}}=\dfrac{\int_{0}^{L}{\left( a+\dfrac{bx}{L} \right)xdx}}{\int_{0}^{L}{\left( a+\dfrac{bx}{L} \right)dx}}$
Performing the integration will be written as,
$\dfrac{7L}{12}=\dfrac{a\dfrac{{{L}^{2}}}{2}+b\dfrac{{{L}^{2}}}{3}}{aL+\dfrac{bL}{2}}$
We can cancel the length term as it is common in both the equations. That is we can write that,
$\dfrac{7}{12}=\dfrac{\dfrac{a}{2}+\dfrac{b}{3}}{a+\dfrac{b}{2}}=\dfrac{\dfrac{3a+2b}{6}}{\dfrac{2a+b}{2}}=\dfrac{3a+2b}{3\left( 2a+b \right)}$
Simplifying the equation further can be written as,
$\dfrac{7}{4}=\dfrac{3a+2b}{\left( 2a+b \right)}$
Now let us rearrange the equation. That is,
$14a+7b=12a+8b$
From this we can reach the final equation. That is,
$2a=b$

So, the correct answer is “Option A”.

Note: In the case of simple rigid bodies with a uniform density, the centre of mass is placed at the centroid. The centre of mass is the specific point at the centre of a distribution of mass in space that is having the characteristics that the weighted position vectors with respect to this point are resulting in being zero.