Question

A uniform thin bar of mass $6\,m$ and length $12L$ is bent to make a regular hexagon. Its moment of inertia about an axis passing through the centre of mass and perpendicular to the plane of a hexagon is:
(A) $20m{L^2}$
(B) $6m{L^2}$
(C) $\dfrac{{12}}{5}m{L^2}$
(D) $30m{L^2}$

Answer 1

In this question, it is asked that the moment of inertia of centre axis, so the moment of inertia is calculated for one side and then it is multiplied with the number of sides, then the moment of inertia of the centre of mass and perpendicular to the plane of a hexagon is determined.

Useful formula:
Moment of inertia about the axis of the hexagon,
$I = \dfrac{{m{L^2}}}{{12}}$
Where, $I$ is the moment of inertia, $m$ is the mass and $L$ is the length

Complete step by step solution:
Mass of the bar is, $m$
The length of the rod is $12L$ and then it is bent, so the length of each side of the hexagon is $2L$.

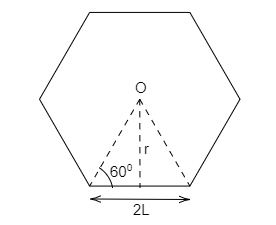
Let the $O$ be the centre mass of hexagon, and $r$ be the perpendicular distance, then
From the figure shown above, consider the right-angled triangle and then by using the trigonometric function, the perpendicular distance can be determined.
From the right-angle triangle,
$\tan \theta = \dfrac{r}{L}\,.......................\left( 1 \right)$
By trigonometry, $\tan \theta$ is equal to the opposite side divided by adjacent sides. Here, the opposite side is $r$ and the adjacent side is $\dfrac{{2L}}{2}$.
From equation (1), the perpendicular distance is given as,
$r = \tan \theta \times L\,..............\left( 2 \right)$
The perfect hexagon has the corner angle of ${120^ \circ }$, here the imaginary triangle is made at the centre of the corner of the hexagon, so the angle is ${60^ \circ }$
By substituting the angle value in equation (2), then
$r = \tan {60^ \circ } \times L$
In trigonometry, the $\tan {60^ \circ }$ is equal to $\sqrt 3$. On substituting this value in the above equation, then
$r = \sqrt 3 L$
The moment of inertia about an axis passing through the centre of mass and perpendicular to the plane of a hexagon is,
$I = \left[ {\dfrac{{m{L^2}}}{{12}} + m{r^2}} \right]\,...................\left( 3 \right)$
This equation shows the moment of inertia about an axis passing through the centre of mass and perpendicular to the plane of a hexagon for one side.
For $6$ side,
$I = 6 \times \left[ {\dfrac{{m{L^2}}}{{12}} + m{r^2}} \right]$
By substituting the $L = 2L$ , which is given in the question and $r$ value in the above equation, then
$I = 6 \times \left[ {\dfrac{{m{{\left( {2L} \right)}^2}}}{{12}} + m{{\left( {L\sqrt 3 } \right)}^2}} \right]$
On squaring the terms, then
$I = 6 \times \left[ {\dfrac{{4m{L^2}}}{{12}} + 3m{L^2}} \right]$
On dividing the terms, then
$I = 6 \times \left[ {\dfrac{{m{L^2}}}{3} + 3m{L^2}} \right]$
Taking the term $6$ inside the bracket, then
$I = \left[ {\dfrac{{6m{L^2}}}{3} + 6 \times 3m{L^2}} \right]$
On further calculation, then the above equation is,
$I = \left[ {2m{L^2} + 18m{L^2}} \right]$
By adding the terms, then
$I = \left[ {20m{L^2}} \right]$
Thus, the above equation shows the moment of inertia about an axis passing through the centre of mass and perpendicular to the plane of a hexagon.

Hence, the option (A) is correct.

Note: In the moment of inertia formula, the extra term $m{r^2}$ is added because, in question it is asked that the moment of inertia about an axis passing through the centre of mass and perpendicular to the plane of a hexagon. So, the term $m{r^2}$ is added with the moment of inertia about an axis passing through the centre of mass.