Question

A uniform square sheet has a side length of $2\;R$. A circular sheet of the maximum possible area is removed from one of the quadrants of the square sheet. The distance of the centre of mass of the remaining portion for, the centre of the original sheet is-
(A) $\dfrac{{\pi R}}{{\sqrt 2 [16 - \pi ]}}$
(B) $\dfrac{R}{{16 - \pi }}$
(C) $\dfrac{R}{{\pi \left[ {16 - \pi } \right]}}$
(D) $\dfrac{{R\pi }}{{16 - \pi }}$

Answer 1

To calculate the distance between the centre of masses in both cases, we consider the circular cut-out section as a separate mass and the rest of the square as a separate second mass. For ease in calculation, assume origin at the centre.
Formula used:
$C{M_x} = \dfrac{{{m_1}{x_1} + {m_2}{x_2} + ... + {m_n}{x_n}}}{{{m_1} + {m_2} + ... + {m_n}}}$
where, $C{M_x}$ is the centre of mass along the X-axis of a body (similar for Y-axis)
${m_i}$is the mass of ${i^{th}}$ point mass of the distributed system.
${x_i}$ is the distance of ${i^{th}}$ point mass of the distributed system.

Complete step by step solution:

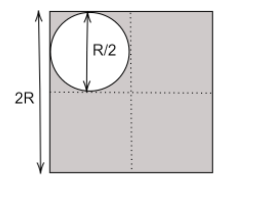
In the given figure, the white circle represents the cutout area, while the grey portion represents the remaining part of the square.
Let us consider the circle as $A$and the rest portion of the square as $B$.
We also assume that the origin is situated in the centre of the square.

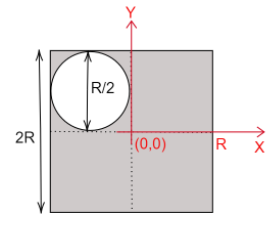
For the square,
The figure is symmetrical about both axes, therefore the center of mass is situated at the midpoint of a given side.
The X-coordinate is $\bar X = 0$
The Y coordinate is $\bar Y = 0$
The centre of mass of the square sheet while still intact is at- $(0,0)$ which is the origin.
Since it is given that the distribution of mass in the sheet is uniform, the mass density (mass per unit area) is constant.
Let $\rho$ be the mass per unit area of the sheet. Then,
$M = \rho a$
where $M$is the mass and $a$ is the area of a given part of the sheet.
The center of mass of a part can now be written in terms of $\rho$ and $a$ as-
$C{M_x} = \dfrac{{\rho {a_1}{x_1} + \rho {a_2}{x_2} + ... + \rho {a_n}{x_n}}}{{\rho {a_1} + \rho {a_2} + ... + \rho {a_n}}}$
$\Rightarrow$ $C{M_x} = \dfrac{{{a_1}{x_1} + {a_2}{x_2} + ... + {a_n}{x_n}}}{{{a_1} + {a_2} + ... + {a_n}}}$
Now if the square sheet is cut into two parts $A$ and $B$ then,
For part $A$ (circular part) the maximum area is possible when the diameter of the circle is $R$, in that case, the centre of mass is situated at the geometrical centre of the circle itself,
With respect to the origin, this distance is,
${\bar X_A} = \dfrac{R}{2}$
${\bar Y_A} = \dfrac{R}{2}$
For part $B$ (leftover part) we assume that the distance of center of mass from the origin is-
${\bar X_B} = {x_B}$
${\bar Y_B} = {y_B}$
We know that the combination of $A$ and $B$ gives the square whose center of mass is $(0,0)$,
Thus equating both of these quantities-
In X-axis,
$0 = \dfrac{{{a_A}{x_A} + {a_B}{x_B}}}{{{a_A} + {a_B}}}$
$\Rightarrow - {a_A}{x_A} = {a_B}{x_B}$
Rearranging,
${x_B} = \dfrac{{ - {a_A}{x_A}}}{{{a_B}}}$
The area ${a_A} = \dfrac{{\pi {R^2}}}{4}$
${x_A} = \dfrac{R}{2}$ (calculated previously)
And,
${a_B} = {\left( {2R} \right)^2} - \dfrac{{\pi {R^2}}}{4}$
(obtained by subtracting the area of a circle from the area of square)
${a_B} = \dfrac{{16{R^2} - \pi {R^2}}}{4}$
The centre of mass,
${x_B} = \dfrac{{ - \left( {\dfrac{{\pi {R^2}}}{4}} \right)\left( {\dfrac{R}{2}} \right)}}{{\dfrac{{16{R^2} - \pi {R^2}}}{4}}}$
Upon simplifying the equation we get,
${x_B} = \dfrac{{ - 4\left( {\pi {R^3}} \right)}}{{8\left( {16{R^2} - \pi {R^2}} \right)}}$
$\Rightarrow {x_B} = \dfrac{{ - \pi R}}{{2\left( {16 - \pi } \right)}}$
Repeating similar steps for the centre of mass along Y-axis, we get-
${y_B} = \dfrac{{\pi R}}{{2(16 - \pi )}}$
Thus the distance of the centre of mass for the new portion from the old centre of mass (origin)-
$D = \sqrt {{x_B}^2 + {y_B}^2}$
Putting the values in this equation,
$D = \sqrt {{{\left( {\dfrac{{ - \pi R}}{{2(16 - \pi )}}} \right)}^2} + {{\left( {\dfrac{{\pi R}}{{2(16 - \pi )}}} \right)}^2}}$
Upon simplifying the equation we get,
$D = \left( {\dfrac{{\sqrt 2 \pi R}}{{2(16 - \pi )}}} \right)$
$\Rightarrow D = \dfrac{{\pi R}}{{\sqrt 2 (16 - \pi )}}$

Hence, option (A) is the correct answer.

Note: A similar approach to this approach, called the “Negative mass” method is also used to calculate the centre of mass of the object when a uniform shape is cut out of a solid object. Mass cannot be negative in real life, but the removed mass may be considered as Negative mass in the calculations.