Question
Question: A uniform sphere of mass M and radius R is surrounded by a concentric spherical shell of same mass b...
A uniform sphere of mass M and radius R is surrounded by a concentric spherical shell of same mass but radius 2R. A point mass m is kept at a distance x (> R) in the region bounded by spheres as shown in the figure. The net gravitational force on the particle is
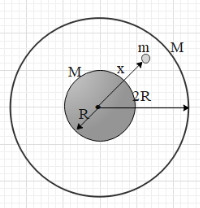
A. x2GMm
B. R2GMmx
C. x2G(M+m)
D. zero
Solution
First, calculate the gravitational force that the solid sphere exerts on the given point mass by using the formula for gravitational force. Then use the concept of shell theory and calculate the force exerted by the shell.
Complete step by step answer:
Let us first calculate the force exerted on the mass m by the solid sphere. The gravitational force on a point mass m located at a distance of x (x > R) from the centre of a sphere of mass M is given as F=x2GMm.
This means that the force exerted by the given solid sphere on the point mass is equal to x2GMm.
Let us now understand about the gravitational force exerted by a spherical shell on a [point mass located inside it. Suppose a point mass is located inside a spherical shell. Now, let us consider the shell made up of small elements of equal masses. Then the point mass will experience gravitational forces due to all the small elements in all the directions such that the net force on the point mass is zero. This concept is according to the shell theory.
Therefore, when a point mass is placed inside a spherical shell, its experiences no force due to the shell.
Hence, in the given case the net force exerted on the point mass m by the shell is zero. This means that the net force experienced by the point mass is equal to x2GMm.
Hence, the correct option is A.
Note: The direction of the gravitational force that a solid sphere exerts on a point mass situated outside the sphere is always towards the centre of mass of the sphere. If the mass of the sphere is uniformly distributed then the centre of mass will be at its geometrical centre.
