Question

A uniform sphere is placed on a smooth horizontal surface and a horizontal force $F$ is applied to it at a distance $h$ above the surface. The acceleration of the centre
A) is maximum when $h=0$
B) is maximum when $h=R$
C) is maximum when $h=2R$
D) is independent of $h$

Answer 1

In order to solve the question, we will first use the relation of velocity, acceleration and time after then we will use the relation of velocity, distance and time then we will substitute the velocity in the relation of acceleration and velocity and from there we will deduce that how acceleration is dependent on $h$.

Formula used:
1. $v = \dfrac{{dx}}{{dt}}$
$v$ is velocity
$x$ is distance
$t$ is time
2. $a = \dfrac{{dv}}{{dt}}$
$a$ is acceleration
$v$ is velocity
$t$ is time

Complete step by step answer:
In the question we are given that a uniform sphere is placed on a smooth horizontal surface and a horizontal force F is applied to it at a distance h above the surface and we have to find the relation of acceleration of the centre with the distance $h$.

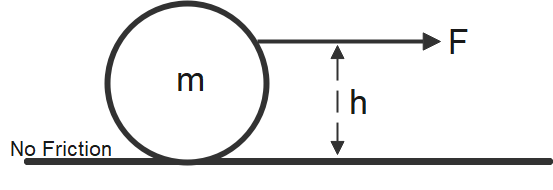
First, we will use the relation between acceleration, velocity and time in order to deduce the relation of acceleration and height we will use the formula
$a = \dfrac{{dv}}{{dt}}$………………… (Equation 1)
In the above relation we will substitute the value of v
Relation of velocity
$v = \dfrac{{dx}}{{dt}}$………………… (Equation 2)
Now we will be substituting the equation 2 in equation 1
$a = \dfrac{d}{{dt}}\left( {\dfrac{{dx}}{{dt}}} \right)$
In the above equation we will find double derivative
$a = \dfrac{{{d^2}x}}{{d{t^2}}}$
And we can also use F = ma, to deduce that same thing as acceleration is dependent on force and mass and not on height
So, from the formula we can find that the acceleration of the centre of mass of the sphere is independent of h, acceleration is independent of h
Hence, the correct option is (D) independent of $h$.

Note: There might be a chance of confusing as $h$ is distance and we have seen that acceleration is dependent on distance x but we have concluded that it doesn’t depend because a on which acceleration is depended in horizontal distance while h is vertical distance on which acceleration doesn’t depends