Question

A uniform sphere has a radius $R$. A sphere of diameter $R$ is cut from its edge as shown. Then the distance of ‘center of mass of remaining portion’ from the ‘center of mass of the original sphere’ is:

Answer 1

The center of mass is a location identified with respect to an individual object or a group of objects (system). Every part of a system is positioned on an average according to the mean of their masses. While dealing with the center of masses we require the mass of each concerned object, but if it is not directly available, then try to derive it from the volume of the object.

Complete step by step answer:
We are given that; the radius of the bigger sphere or outer sphere is $R$. Then another smaller sphere or inner sphere has its diameter as $R$, so its radius will be half of its diameter. This means that the smaller sphere will have its radius as $\dfrac{R}{2}$.

Let us reconstruct the given diagram and mark the radius of each sphere as well as their centers, this will make it easier to solve the problem; Let the center of the bigger sphere be ‘$O$’, let us mark the radius of the outer or bigger sphere, $AO$ (as shown in the figure) as $R$, let the center of the smaller or inner circle be ‘$C$’, and let the diameter of the smaller circle, $OB$, be $R$; then its radius is marked as $OC = \dfrac{R}{2}$.

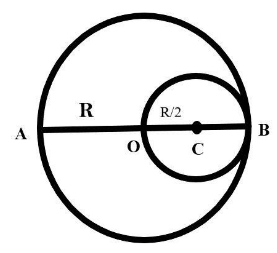
We are required to find the distance between center of mass of (original sphere + remaining portion);
Let the unknown distance be denoted as ‘$s$’. Now in order to find the required distance, we need to establish a relationship between the positions of the center of mass. Also for this we initially require the mass of the individual spheres and remaining portion;

We know that mass is the product of density and volume of the sphere. Let the sphere be of density ‘$d$’. And let us write down the volume of each sphere;
Volume of outer or bigger sphere or radius $R$ $= \dfrac{4}{3}\pi {R^3}$
Volume of inner or smaller sphere of radius $\dfrac{R}{2}$ $= \dfrac{4}{3}\pi {\left( {\dfrac{R}{2}} \right)^3}$
Then the mass of each sphere is as follows;
Mass of the bigger sphere (or complete sphere) $= \dfrac{4}{3}\pi {R^3} \times d$
Mass of the smaller sphere (or inner sphere) $= \dfrac{4}{3}\pi {\left( {\dfrac{R}{2}} \right)^3} \times d$
We need to find the mass of the remaining object also because we are finding the relation of center of mass between the remaining object and complete sphere.
So mass of remaining part $= \dfrac{7}{6}\pi {R^3} \times d$

But remember that the center of mass’s position for the bigger sphere or total sphere is $0$. This is calculated with respect to the inner sphere and the remaining part of the sphere.
So the equation can be written as:
$\Rightarrow$Position of complete sphere’s center of mass $= 0$
$\Rightarrow \dfrac{{{m_1} \times {s_1} + {m_2} \times {s_2}}}{{{m_1} + {m_2}}} = 0 \to (i)$
Here:
${m_1} =$ mass of remaining sphere $= \dfrac{7}{6}\pi {R^3} \times d$, ${m_2} =$ mass of inner sphere $= \dfrac{4}{3}\pi {\left( {\dfrac{R}{2}} \right)^3} \times d$
${s_1} =$ distance of center of mass of remaining part from the complete sphere $= - x$
${s_2} =$ distance of center of inner sphere to the center of complete sphere $= \dfrac{R}{2}$

Since both the distances are taken in opposite directions, one of the distances must take an opposite sign. So let ‘${s_1}$’ be negative, then the equation $(i)$ becomes:
$\Rightarrow \dfrac{{\left( {\dfrac{7}{6}\pi {R^3} \times d \times ( - s)} \right)\; + \;\left( {\dfrac{4}{3}\pi {{\left( {\dfrac{R}{2}} \right)}^3} \times d \times \left( {\dfrac{R}{2}} \right)} \right)}}{{\left( {\dfrac{7}{6}\pi {R^3} \times d + \dfrac{4}{3}\pi {{\left( {\dfrac{R}{2}} \right)}^3} \times d} \right)}} = 0$
Simplifying we get:
$\Rightarrow \left( {\dfrac{7}{6}\pi {R^3} \times d \times ( - s)} \right)\; + \;\left( {\dfrac{4}{3}\pi {{\left( {\dfrac{R}{2}} \right)}^3} \times d \times \left( {\dfrac{R}{2}} \right)} \right) = 0$
$\therefore \dfrac{R}{{14}} = s$

So the required distance of the center of mass of the remaining part from the total sphere will be $\dfrac{R}{{14}}$.

Note: Determining the position of the center of mass is critical since it helps you to interpret dynamic questions dependent on the center of mass's motion. Consider an object thrown into the air, say a hammer, then the center of mass of that hammer (which cannot be changed) would take a parabolic direction, even though the hammer on its own rotates in different directions.