Question

A uniform sphere has a mass $M$ and a radius $R$. Find the pressure $\overrightarrow{p}$ inside the sphere, caused by gravitational compression, as a function of the distance $r$ from its center. Evaluate $\overrightarrow{p}$ at the center of the earth, assuming it to be a uniform sphere.

Answer 1

The constant force of gravity experienced by the massive body results in the development of an effect called gravitational compression. We will use the expression for the gravitational force experienced by a massive body and determine the pressure at the center of the earth by using the pressure-force relationship.

Complete step by step answer:
Gravitational compression is described as a phenomenon in which gravitational force, acting on the mass of an object, compresses it and reduces its size which results in increasing the density of the object.
We are given a uniform sphere that has a mass $M$ and a radius of $R$. Let’s say its mass density is $\rho$.

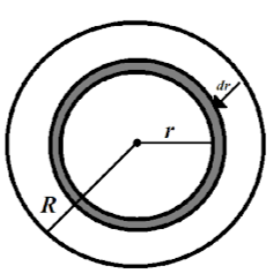
We have partitioned the solid sphere into thin spherical layers and consider a layer of thickness $dr$ lying at a distance $r$ from the center of the ball. Each spherical layer possesses on the layers within it. The considered spherical layer is attracted to the part of the sphere lying within it. The outer part of the sphere will not act on it.
Therefore, for a spherical layer of thickness $dr$ at a distance $r$ from the centre of the ball,
$dF=dP\cdot 4\pi {{r}^{2}}$
Where,
$dF$ is the force experienced by the spherical layer
$dP$ is the amount of pressure acting on the spherical layer
$4\pi {{r}^{2}}$ is the area of the spherical layer
Or,
$dP\cdot 4\pi {{r}^{2}}=\dfrac{G\left( \dfrac{4}{3}\pi {{r}^{3}}\rho \right)\left( 4\pi {{r}^{2}}dr\rho \right)}{{{r}^{2}}}$
Where,
$\rho$ is the mean density of the sphere
$G$ is the gravitational constant
$dP=\dfrac{4}{3}\pi G{{\rho }^{2}}rdr$
Thus,
$P=\int\limits_{r}^{R}{dP}$
Put, $dP=\dfrac{4}{3}\pi G{{\rho }^{2}}rdr$
We get,
$P=\int\limits_{r}^{R}{\dfrac{2\pi }{3}G{{\rho }^{2}}\left( {{R}^{2}}-{{r}^{2}} \right)}$
The pressure will be vanished at$r=R$
Put, $P=\dfrac{M}{\dfrac{4}{3}\pi {{R}^{3}}}$
$P=\dfrac{3}{8}\left( 1-\dfrac{{{r}^{2}}}{{{R}^{2}}} \right)\dfrac{G{{M}^{2}}}{\pi {{R}^{4}}}$
Now,
By putting $r=0$, we will get the pressure at the sphere’s centre
For finding the pressure at the centre of earth,
$\begin{aligned} & M=5.972\times {{10}^{24}}Kg \\\ & \rho =5.5\times {{10}^{3}}kg{{m}^{-3}} \\\ & R=6400Km=6.4\times {{10}^{6}}m \\\ \end{aligned}$
$\begin{aligned} & P=\dfrac{3}{8}\left( 1-\dfrac{{{r}^{2}}}{{{R}^{2}}} \right)\dfrac{G{{M}^{2}}}{\pi {{R}^{4}}} \\\ & P=\dfrac{3}{8}\times \dfrac{6.67\times {{10}^{-11}}\times {{\left( 5.972\times {{10}^{24}} \right)}^{2}}}{\dfrac{22}{7}\times {{\left( 6.4\times {{10}^{6}} \right)}^{4}}} \\\ \end{aligned}$
We get,
$\begin{aligned} & P=1.73\times {{10}^{11}}Pa \\\ & P=1.72\times {{10}^{6}}atms \\\ \end{aligned}$

Note: In the core or center of a star such as the Sun, the gravitational pressure can be balanced by the outward thermal pressure from the fusion reactions, temporarily halting the effect of gravitational compression. At the center of a star or planet, gravitational compression can produce heat as well.