Question
Question: A uniform solid sphere of mass \(1kg\) and radius \(10cm\) is kept stationary on a rough inclined pl...
A uniform solid sphere of mass 1kg and radius 10cm is kept stationary on a rough inclined plane by fixing a highly dense particle at B. Inclination of the plane is 37o with horizontal and AB is the diameter of the sphere which is parallel to the plane, as shown in the figure. Then,
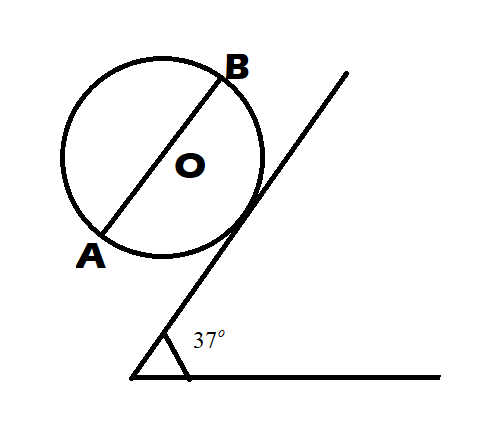
A. Mass of the particle fixes at B is 4kg
B. Mass of the particle fixes at B is 3kg
C. Minimum required coefficient of friction between sphere and the plane to keep in equilibrium is μmin=0.75
D. Minimum required coefficient of friction between sphere and the plane to keep in equilibrium is μmin=0.5
Solution
This is a great question as per standards. First we have to assume the mass of the particle. Then we have to make the free body diagram and mention all the forces. After than to obtain the limiting condition of friction, we have to find the forces along the normal and along the plane. Then we can just put them under the formula and then get the answer.
Complete step by step answer:
Firstly we have to sort out what we have got :
Mass of uniform solid sphere : 1kg
Radius of uniform solid sphere : 10cm
Inclination of the plane : 37o
Step1: We have to assume the mass of the particle as m. Now, it is most important to make the free body diagram of the system with all the forces mentioned so that we can work on the forces.
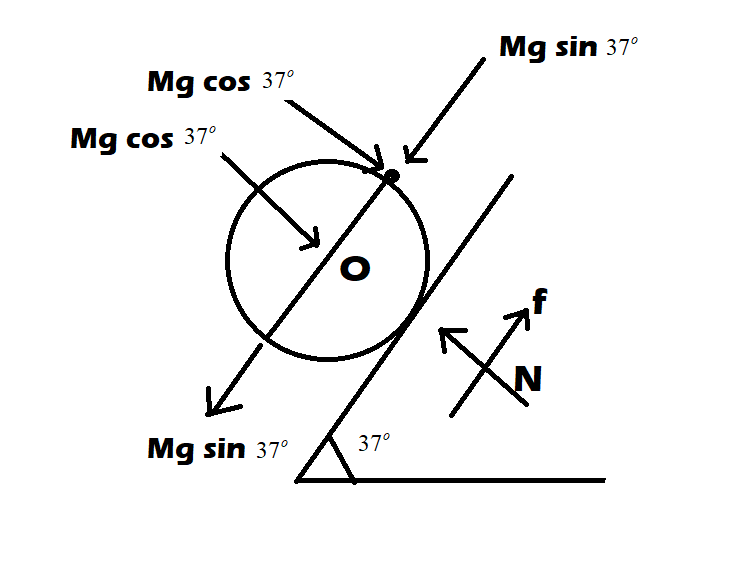
By the system we can observe that the given system is in a state of equilibrium, thus the net torque would be zero.
Step 2: Therefore, we have to equate all the torque acting on the system. Taking torque of point A of all the forces acting on system:
(Mgsin37o)R+(mgsin37o)R=(mgcos37o)R ⇒(1×10×53)+(m×10×53)=(m×10×54) ⇒6+6m=8m ⇒2m=6 ⇒m=3kg
Therefore the mass is 3kg
Step 3: The friction force between the sphere and the plane is static in nature so:
Forces along the normal would be :-
⇒N=Mgcos37o+mgcos37o ⇒N=1×10×54+3×10×54 ⇒N=(8+24)N ⇒N=32N
And the forces along the plane would be:-
f=Mgsin37o+mgsin37o ⇒f=1×10×53+3×10×53 ⇒f=(6+18)N ⇒f=24N
Therefore by the formula of μmin we will get:
μmin=Nf ⇒μmin=3224 ⇒μmin=0.75
Hence, the value of μmin=0.75
Therefore, the correct options would be B and C
Note:- The forces along the plane and normal should be calculated considering the direction. If the forces go against each other the difference should take place whereas in the same direction they should be summed.
