Question

A uniform solid right circular cone of base radius r is joined to a uniform solid hemisphere of radius r and of the same density, as shown. The center of mass of the composite solid lies at the center of the base of the cone. The height of cone is

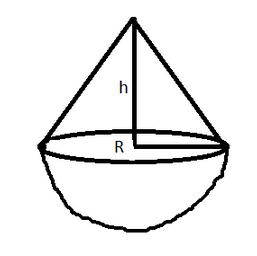
$A.$ 1.5r
$B.$ $\sqrt 3$r
$C.$ 3r
$D.$ $2\sqrt 3$r

Answer 1

HINT- The center of mass of a body or a system of bodies is a mean position of the total weight of the body where the resultant of the forces applied is considered to be acted upon such that forces, momentum and energy are conserved. The body or system of bodies is balanced around the center of mass and the average of the weighted position coordinates defines its coordinates.

Now from the question, we have
The figure is shown below-

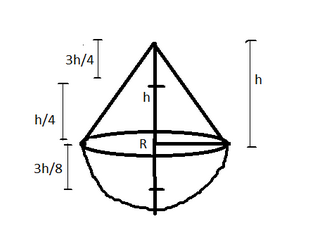
Volume of cone = $\dfrac{1}{3}\pi {r^3}h$
Mass of cone, ${m_1} = \rho \times \dfrac{1}{3}\pi {r^2}h$
Mass of hemisphere, ${m_2} = \rho \times \dfrac{1}{2} \times \dfrac{4}{3}\pi {r^3}$ = $\rho \times \dfrac{2}{3}\pi {r^3}$
Now, $Y = \dfrac{{{m_1}{y_1} + {m_2}{y_2}}}{{{m_1} + {m_2}}}$
$0 = \dfrac{{\rho \times \dfrac{1}{3}\pi {r^2}h \times \dfrac{h}{4} + \rho \times \dfrac{2}{3}\pi {r^3}( - \dfrac{{3r}}{8})}}{{\rho \times \dfrac{1}{3}\pi {r^2}h + \rho \times \dfrac{2}{3}\pi {r^3}}}$
Or, $\rho \times \dfrac{1}{3}\pi {r^2}[\dfrac{{{h^2}}}{4} - 2r \times \dfrac{{3r}}{8}] = 0$
Or $\dfrac{{{h^2}}}{4} - \dfrac{{3{r^2}}}{4} = 0$ or $h = \sqrt 3 r$
Therefore, the correct option is $B.$

NOTE- More about center of mass-
The center of mass of a distribution of mass in space is the unique point where the weighted relative position of the distributed mass sums zero. This is the point to which a force may be applied to cause a linear acceleration without an angular acceleration. Calculations in mechanics are often simplified when formulated with respect to the center of mass. It is a hypothetical point where the entire mass of an object may be assumed to be concentrated to visualize its motion. In other words, the center of mass is the particle equivalent of a given object for application of Newton’s laws of motion.
In case of a single rigid body, the center of mass is fixed in relation to the body, and if the body has uniform density, it will be located at the centroid. The center of mass may be located outside the physical body, as is sometimes the case for hollow or open-shaped objects, such as horseshoe. In case of a distribution of separate bodies, such as the planets of the Solar System, the center of mass may not correspond to the position of any individual member of the system.