Question

A uniform solid block has a weight of 500N, width $0.4m\;$ , and height $0.6m$ . The block rests on the edge of a step of depth 0.8m, as shown. The block is knocked over the edge of the step and rotates through $90^\circ$ before coming to rest with the $0.6m$ edge horizontal. What is the change in gravitational potential energy of the block?

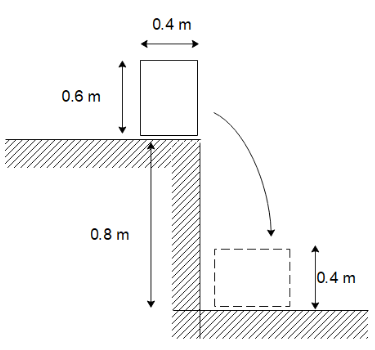
A) 300 J
B) 400 J
C) 450 J
D) 550 J

Answer 1

The potential energy of an object is determined by its height above the ground. The centre of mass of the uniform solid block will lie at its geometrical centre.

Formula used
In this solution, we will use the following formula
$U = mgh$ where $U$ is the potential energy of the object, whose mass is $m$ , gravitational acceleration $g$ and is at a height h

Complete step by step answer:
We’ve been given a uniform solid block of weight 500 N. The potential energy of the block will due to its height. To calculate the potential energy of the block, we should consider the solid block to be a point object of weight 500 N that lies at the geometrical center of the block.
At the top position, the centre of mass of the block will be at a height of
${h_1} = 0.8\,m + \dfrac{{0.6}}{2}m$
$\Rightarrow {h_1} = 1.1\,m$
Hence the potential energy of the object can be calculated as
${U_1} = mg{h_1} = W{h_1}$ where $W$ is the weight of the block.
Hence, ${U_1} = 500 \times 1.1\,$
$\Rightarrow {U_1} = 550\,N$
When the block falls, we can see that the centre of the mass lies at a height of
${U_2} = W{h_2}$
$\Rightarrow {U_2} = 500 \times 0.2 = 100N$
Hence the change in potential energy can be calculated as
$\Delta U = {U_1} - {U_2}$
$\Rightarrow \Delta U = 550 - 100$
Which gives us
$\Delta U = 450J$ which corresponds to option (C).

Note:
We should realize that the mass of the block can instead be replaced by a point object having a weight equal to the weight of the block. This point mass will lie at the centre of mass of the block and it will be easier for us to calculate the potential energy for a point mass.