Question

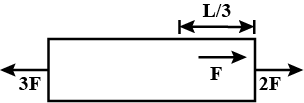
A uniform slender rod of length $L$ , cross-sectional area $A$ and Young's modulus $Y$ is acted upon by the forces shown in the figure. The elongation of the rod is:
$(A)\dfrac{{3FL}}{{5AY}}$
$(B)\dfrac{{2FL}}{{5AY}}$
$(C)\dfrac{{3FL}}{{8AY}}$
$(D)\dfrac{{8FL}}{{3AY}}$

Answer 1

Young's modulus $Y$ , which is also known as the modulus of elasticity in tension, is a mechanical property of matter that measures the tensile stiffness of a solid material. In simple words, we can also say that it is a measure of elasticity, equal to the ratio of the stress acting on a substance to the strain produced.

Complete step by step solution:
When forces pull on an object and cause its elongation, like the stretching of an elastic band, we call such stress a tensile stress. In such a case, when deforming forces act tangentially to the object's surface, we call them 'shear' forces and the stress they cause is called shear stress.
Tensile (or compressive) stress causes elongation (or shortening) of the object or medium and is due to an external force acting along only one direction perpendicular to the cross-section. Bulk strain is the response of an object or medium to bulk stress.
According to the given diagram, we can clearly see that the rod is divided into two parts of length $\dfrac{L}{3}$ and $\dfrac{{2L}}{3}$ .
So, we will solve this question for the two parts of rods separately.
We can clearly see that the force acting on both the sides of the part $\dfrac{{2L}}{3}$ is $3F$
So the extension $x = \dfrac{{8FL}}{{3AY}}$ ${x_1} = \dfrac{{\left[ {3F \times \dfrac{{2L}}{3}} \right]}}{{AY}}.......(1)$
Similarly, the force acting on both the sides of part $\dfrac{L}{3}$ is $2F$
So the extension ${x_2} = \dfrac{{\left[ {2F \times \dfrac{L}{3}} \right]}}{{AY}}.......(2)$
Now the total extension will be calculated by adding equation (1) and (2),
$x = {x_1} + {x_2}$
$x = \dfrac{{\left[ {3F \times \dfrac{{2L}}{3}} \right]}}{{AY}} + \dfrac{{\left[ {2F \times \dfrac{L}{3}} \right]}}{{AY}}$
On simplifying the above equation, we get,
$x = \dfrac{{8FL}}{{3AY}}$
So, the final answer is $(D)\dfrac{{8FL}}{{3AY}}$ .

Note:
The insight that Young's modulus represents the strength of the bonds between all the atoms in a crystal has a first important consequence for the elastic properties of sword blades. A few percent of other bonds, for example to carbon atoms in steel, will at best make a difference of a few percent in Young's modulus.