Question
Question: A uniform slender rod of length $l$ and mass $m$ is rigidly to a circular hoop of radius $l$ as show...
A uniform slender rod of length l and mass m is rigidly to a circular hoop of radius l as shown. The mass of the hoop is negligible. If the rod and hoop are released from rest on a fixed horizontal surface in the position illustrated, determine the initial value of the friction force F. if friction is sufficient to prevent slipping.
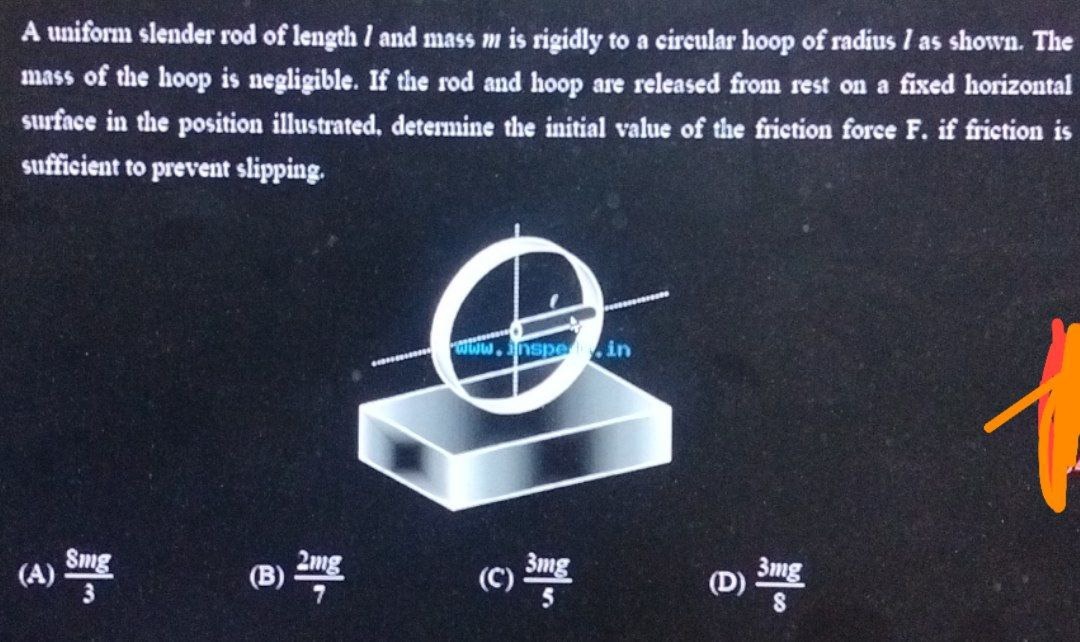
38mg
72mg
53mg
83mg
83mg
Solution
We solve the problem by “rotating‐about the instantaneous axis” (point of contact P). In our analysis we assume that the rod is initially horizontal. (This is what the diagram implies.) Then:
-
Choose coordinates so that the circular hoop (radius l) touches the floor at point P = (0,0). Its center is at O = (0,l) and the rod is rigidly attached so that, being horizontal, its center-of-mass (of the uniform rod of length l) is at
G = O + (l/2, 0) = (l/2, l). -
The only external force with a moment about P is the weight mg acting vertically downward at G. The torque about P is
τ=mg×(\mboxhorizontaldistancefromP\mboxtolineofactionofmg)=mg×2l=2mgl. -
The assembly rotates about P; we compute the moment of inertia by the parallel‐axis theorem. The rod’s moment of inertia about its center for rotation about an axis perpendicular to it is
Icm=121ml2.The distance from G to P is
d=(2l)2+l2=2l5.Thus,
IP=Icm+md2=121ml2+m(2l5)2=121ml2+45ml2=12ml2(1+15)=1216ml2=34ml2. -
The angular acceleration about P is
α=IPτ=(4ml2/3)(mgl/2)=8l3g. -
Since the whole body rotates about P, each point moves in a circle centered at P. The center-of-mass G is at a distance d=2l5 and its tangential acceleration is dα. However, using geometry one may show that the horizontal component of this acceleration equals exactly
ax=lα=83g.(Details: The tangent to the circle at G is perpendicular to PG=(l/2,l); working out its components gives ax=α(l5/2)(2/5)=lα.)
-
The only horizontal force on the body is the friction force F. By Newton’s second law,
F=max=m(83g)=83mg.
Thus the initial friction force is 83mg. This corresponds to option (D).
Explanation (minimal):
- Choose P as instantaneous axis (contact point).
- The weight mg at the rod’s COM (at (l/2,l)) gives a torque τ=2mgl.
- Using parallel‐axis theorem, the moment of inertia about P is IP=34ml2.
- Therefore, α=8l3g.
- The horizontal acceleration of the COM is ax=lα=83g.
- So, F=max=83mg.
