Question
Question: A uniform rope of length \[L\] is pulled by a fixed force \[F\] as represented in the figure. What w...
A uniform rope of length L is pulled by a fixed force F as represented in the figure. What will be the tension in the rope at distance x from the end where the force is applied?
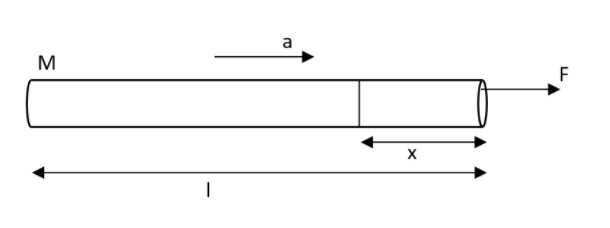
Solution
First of all find the acceleration of the rope. The acceleration can be found by taking the ratio of the force to the mass of the body. Then find the mass per unit length of the rope. For this part the tension can be found by taking the product of the mass of the body and the acceleration of the body. Substitute the values in it. This will help you in answering this question.
Complete step by step answer:
The acceleration can be found by taking the ratio of the force to the mass of the body. That is we can write that,
a=MF
The mass per unit length can be shown as,
λ=lM
Therefore the mass of the part of length (l−x) can be found by the equation,
m=λ(l−x)
Where the mass per unit length can be substituted as,
m=lM(l−x)
For this part the tension can be found by taking the product of the mass of the body and the acceleration of the body. That is we can write that,
T=ma
Substituting the values in it will give,
T=ma=lM(l−x)MF
Simplifying this equation will give,
T=lF(l−x)
Therefore the tension in the rope at distance x from the end where the force is applied has been found. Therefore the answer has been obtained.
Note:
Tension is basically the force itself. It can be explained as the pulling force which has been axially transmitted using the ways of a cable, a string, chain, or similar one-dimensional continuous object or a rope. The unit of tension is the same as that of force itself.
