Question

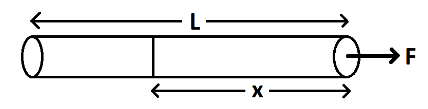
A uniform rope of length $L$ is pulled by a constant force $F$ as shown. What is the tension in the rope at distance $x$ from the end where the force is applied?

Answer 1

When a heavy rope (rope having mass) is being pulled or a force is applied on them then different portions of rope have different tensile force (tension).Tension is nothing but a force experienced by the rope which pulls it or creates a pulling force.

Complete step by step answer:
Given: Length of rope = $L$, Force applied on the rope = $F$.
As the mass is not mentioned, let the mass of the rope be $M$ kg.
Mass per unit length (say $\lambda$) $\therefore \,\,\lambda \,=\,\dfrac{M}{L}$.
Mass as a function of $x$ = Mass per unit length$\times$ Length of rope
$\therefore \,\,m(x)\,\,=\,\,\lambda \times l\,=\,\dfrac{M}{L}\times x$
We need to find tension in the rope as a function of $x$ from the front end.
As the rope has force on only one side so the rope is not in equilibrium.
Hence the rope will have an acceleration.
So, Acceleration of the rope: $a\,=\,\dfrac{F}{M}$.
The tension force is different on different parts of the rope.

Explanation:
If we take a section of rope which is beyond the distance $x$ from the front end.
Force acting on that section of rope is only the tension force. If we increase the value of $x$, the mass of the section decreases and vice versa. But the acceleration of the section will remain the same. From Newton’s second law: $F\,\,=\,\,m\,a$,

If acceleration remains constant then Force is directly proportional to the mass. Hence force will be different on different parts of the rope depending upon the mass that the force has to pull. Here also the same concept applies and Tension in the rope ($T(x)$) varies as its distance from the front end varies.

Let’s analyse at the cross section which is a distance of $x$ from the front end.
Let the tension force there to be $T(x)$ that these two portions will apply on each

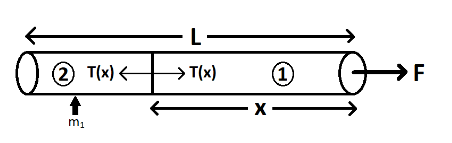
Now for part 1:
Mass of part 1 =$\,\lambda \times x\,=\,\,\frac{M}{L}\times x$
Acceleration of part 1 = $a\,=\,\frac{F}{M}$
Now, Applying Newton’s law of motion:

$F\,-\,T(x)\,\,=\,\,{{m}_{1}}\,\times \,a$
$\Rightarrow \,\,F\,-\,\,T(x)\,\,=\,\,\,\left( \dfrac{M}{L}\times x \right)\times \dfrac{F}{M}$
$\Rightarrow \,\,F\,-\,\dfrac{Fx}{L}\,\,=\,\,\,T(x)\,$
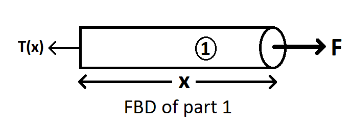
$\Rightarrow \,\,F\left( 1-\dfrac{x}{L} \right)\,\,=\,\,T(x)$
$\therefore \,\,F\left( \dfrac{L-x}{L} \right)\,\,=\,\,T(x)$

Hence, the tension in the rope at distance $x$ from the end is $F\left( \dfrac{L-x}{L} \right)$.

Note: Take care of the distance $x$ from which end it is taken in the question. Sometimes the $x$ is taken from the other end which changes the whole answer. Take care of the sign also keeping in view the direction you are choosing.