Question

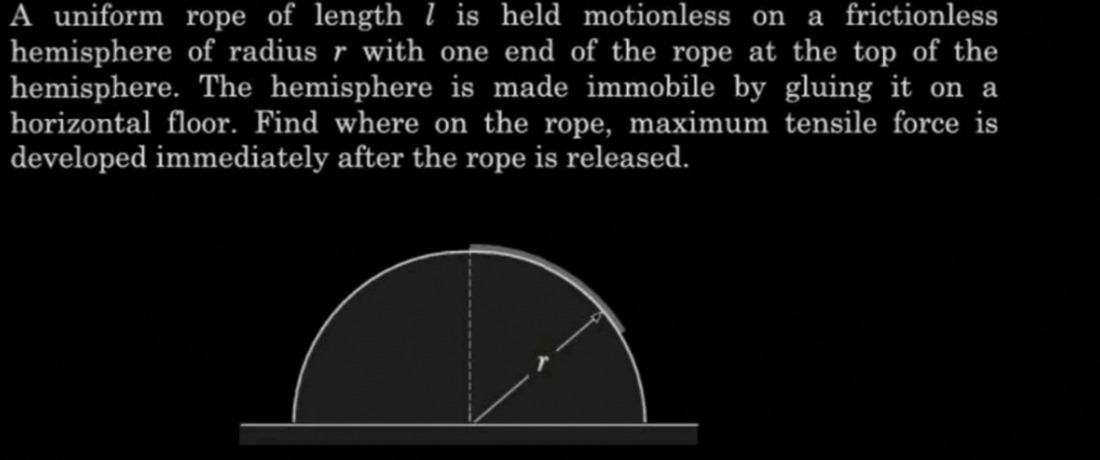
A uniform rope of length $l$ is held motionless on a frictionless hemisphere of radius $r$ with one end of the rope at the top of the hemisphere. The hemisphere is made immobile by gluing it on a horizontal floor. Find where on the rope, maximum tensile force is developed immediately after the rope is released.

Answer 1

at a distance $r\theta_m$ from the top end, where $\sin\theta_m = \frac{1 - \cos(l/r)}{l/r}$

Answer 2

To find the maximum tensile force, we first determine the acceleration of the rope and then derive an expression for the tension at any point along the rope.

1. Define Variables and Coordinate System: Let $\lambda$ be the linear mass density of the uniform rope (mass per unit length).
Let the angle $\theta$ be measured from the vertical axis (top of the hemisphere) downwards.
The rope extends from $\theta = 0$ to $\theta = \phi_{max}$, where $l = r\phi_{max}$. So, $\phi_{max} = l/r$.

2. Determine the Acceleration of the Rope:
Since the rope is inextensible and frictionless, all points on the rope will have the same tangential acceleration, say $a$.
Consider the entire rope as a system. The total mass of the rope is $M = \lambda l = \lambda r \phi_{max}$.
The only force causing the rope to slide is the tangential component of gravity acting on each element of the rope.
The tangential component of gravitational force on a small element of mass $dm = \lambda ds = \lambda r d\theta$ at angle $\theta$ is $dm \cdot g \sin\theta = \lambda r g \sin\theta d\theta$.

The total tangential force on the entire rope is the integral of these components from $\theta = 0$ to $\theta = \phi_{max}$: $F_{total, tangential} = \int_{0}^{\phi_{max}} \lambda r g \sin\theta d\theta$
$F_{total, tangential} = \lambda r g [-\cos\theta]_{0}^{\phi_{max}}$
$F_{total, tangential} = \lambda r g (-\cos\phi_{max} - (-\cos0))$
$F_{total, tangential} = \lambda r g (1 - \cos\phi_{max})$

Using Newton's second law for the entire rope: $F_{total, tangential} = M a$
$\lambda r g (1 - \cos\phi_{max}) = (\lambda r \phi_{max}) a$
$a = \frac{g (1 - \cos\phi_{max})}{\phi_{max}}$

3. Derive the Expression for Tension $T(\theta)$:
Consider a segment of the rope from an arbitrary point at angle $\theta$ down to the free end at $\phi_{max}$.
Let $T(\theta)$ be the tension at angle $\theta$. This tension acts upwards (towards the top of the hemisphere).
The mass of this segment is $M_{segment} = \lambda \times (\text{length of segment}) = \lambda r (\phi_{max} - \theta)$.
The forces acting on this segment are $T(\theta)$ upwards and the tangential components of gravity on all elements within this segment, acting downwards.
Applying Newton's second law to this segment:
$\sum F_{tangential} = M_{segment} \cdot a$
The sum of tangential components of gravity on the segment is:
$\int_{\theta}^{\phi_{max}} \lambda r g \sin\alpha d\alpha = \lambda r g [-\cos\alpha]_{\theta}^{\phi_{max}}$
$= \lambda r g (\cos\theta - \cos\phi_{max})$

So, the equation of motion for the segment is:
$\lambda r g (\cos\theta - \cos\phi_{max}) - T(\theta) = \lambda r (\phi_{max} - \theta) a$

Rearranging to solve for $T(\theta)$:
$T(\theta) = \lambda r g (\cos\theta - \cos\phi_{max}) - \lambda r (\phi_{max} - \theta) a$

Substitute the expression for $a$:
$T(\theta) = \lambda r g (\cos\theta - \cos\phi_{max}) - \lambda r (\phi_{max} - \theta) \frac{g (1 - \cos\phi_{max})}{\phi_{max}}$
$T(\theta) = \lambda r g \left[ (\cos\theta - \cos\phi_{max}) - \frac{(\phi_{max} - \theta)}{\phi_{max}} (1 - \cos\phi_{max}) \right]$

4. Find the Position of Maximum Tension:
To find the position where the tension is maximum, we differentiate $T(\theta)$ with respect to $\theta$ and set the derivative to zero:
$\frac{dT}{d\theta} = \lambda r g \left[ -\sin\theta - \frac{(-1)}{\phi_{max}} (1 - \cos\phi_{max}) \right]$
$\frac{dT}{d\theta} = \lambda r g \left[ -\sin\theta + \frac{(1 - \cos\phi_{max})}{\phi_{max}} \right]$

Set $\frac{dT}{d\theta} = 0$:
$-\sin\theta + \frac{(1 - \cos\phi_{max})}{\phi_{max}} = 0$
$\sin\theta = \frac{1 - \cos\phi_{max}}{\phi_{max}}$

Let $\theta_m$ be the angle where maximum tension occurs.
So, $\sin\theta_m = \frac{1 - \cos(l/r)}{l/r}$.

The maximum tension is developed at a point on the rope that is at an angular position $\theta_m$ from the top of the hemisphere, where $\theta_m$ satisfies the equation above.
The distance along the rope from the top of the hemisphere to this point is $s = r\theta_m$.

Summary of the location:
The maximum tensile force is developed at a point on the rope at an angle $\theta_m$ from the top of the hemisphere, such that: $\sin\theta_m = \frac{1 - \cos(l/r)}{l/r}$ This corresponds to a distance $s = r\theta_m$ from the top end of the rope.

The conditions for the rope to remain on the hemisphere require $\phi_{max} \le \pi/2$ (i.e., $l \le r\pi/2$), as the normal force becomes zero for $\theta > \pi/2$. The problem implies the rope is on the hemisphere.