Question

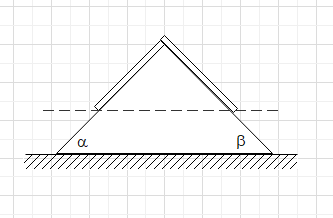
A uniform rope of length L and mass M is placed on a smooth fixed wedge as shown. Both ends of rope are at the same horizontal level. The rope is initially released from rest, then the magnitude of initial acceleration of the rope is

Answer 1

To solve this question, first find the component of the forces acting on the ropes on both sides and then equate them to find the equation. Add the equations for both sides of the rope to find the initial acceleration acting on the rope.

Complete step-by-step answer:
The length of the rope on the left side is ${{L}_{1}}$ and on the right side is ${{L}_{2}}$. The total length of the rope is L.
$L={{L}_{1}}+{{L}_{2}}$
Total mass of the rope is M.
The mass per unit length of the rope is $\dfrac{M}{L}$
So, the mass of the rope on the left side is ${{m}_{1}}={{L}_{1}}\dfrac{M}{L}$
Mass of the rope on the right side is ${{m}_{2}}={{L}_{2}}\dfrac{M}{L}$

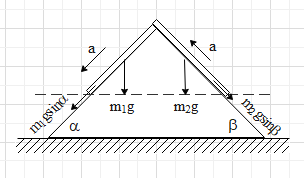
Weight of the rope on the left side is, ${{m}_{1}}g=\dfrac{{{L}_{1}}M}{L}g$
Weight of the rope on the right side is, ${{m}_{2}}g=\dfrac{{{L}_{2}}M}{L}g$
Now, taking the component of the forces on the ropes,
On the left side of the rope,
$\begin{aligned} & {{m}_{1}}g\sin \alpha -T={{m}_{1}}a \\\ & \dfrac{{{L}_{1}}M}{L}\sin \alpha -T=\dfrac{{{L}_{1}}M}{L}a \\\ \end{aligned}$
And, on the right side of the rope,
$\begin{aligned} & T-{{m}_{2}}g\sin \beta ={{m}_{2}}a \\\ & T-\dfrac{{{L}_{2}}M}{L}g\sin \beta =\dfrac{{{L}_{2}}M}{L}a \\\ \end{aligned}$
Adding the above two equations,
$\begin{aligned} & \dfrac{{{L}_{1}}M}{L}g\sin \alpha -\dfrac{{{L}_{2}}M}{L}g\sin \beta =\dfrac{{{L}_{1}}M}{L}a+\dfrac{{{L}_{2}}M}{L}a \\\ & \left( {{L}_{1}}\sin \alpha -{{L}_{2}}\sin \beta \right)g=\left( {{L}_{1}}+{{L}_{2}} \right)a=La \\\ & a=\dfrac{\left( {{L}_{1}}\sin \alpha -{{L}_{2}}\sin \beta \right)g}{a} \\\ \end{aligned}$
Now, since both ends of the rope are in the same horizontal line or in the same vertical height, the components,
${{L}_{1}}\sin \alpha ={{L}_{2}}\sin \beta$
So, we can write,
$a=0$

So, the correct answer is “Option A”.

Note: In the above question, the angles of the triangle are different from each other and also the lengths of the rope on the both sides are also different. But then also the components in the vertical directions are equal to each other because the both ends of the rope are in the same horizontal plane or in the same vertical height.