Question

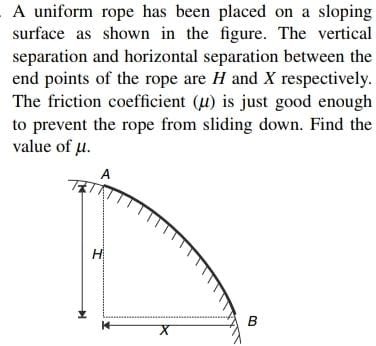
A uniform rope has been placed on a sloping surface as shown in the figure. The vertical separation and horizontal separation between the end points of the rope are H and X respectively. The friction coefficient ($\mu$) is just good enough to prevent the rope from sliding down. Find the value of $\mu$.

• A. $\frac{X}{H}$
• B. $\frac{H}{X}$
• C. $\frac{\sqrt{X^2 + H^2}}{X}$
• D. $\frac{X}{\sqrt{X^2 + H^2}}$

Answer 1

Answer: (B)

$\frac{H}{X}$

Answer 2

Let the rope have a mass $M$ and length $L$. For the rope to be in equilibrium and just about to slide down, the total component of gravitational force acting along the tangent of the rope downwards must be balanced by the maximum static friction force acting upwards along the tangent.

Consider a small element of the rope of mass $dm$. The gravitational force on this element is $dm \cdot g$ acting vertically downwards. Let $\theta$ be the angle of the tangent to the rope with the horizontal at a particular point.

The component of gravity acting along the tangent (downwards) is $dm \cdot g \sin\theta$. The component of gravity acting perpendicular to the tangent (inwards) is $dm \cdot g \cos\theta$. The normal force $dN$ exerted by the surface on the element is equal in magnitude to the perpendicular component of gravity, so $dN = dm \cdot g \cos\theta$.

The static friction force $df_s$ acts upwards along the tangent, opposing the motion. Since the friction is just enough to prevent sliding, it is at its maximum value: $df_s = \mu dN = \mu dm \cdot g \cos\theta$.

For equilibrium, the sum of forces along the tangent must be zero. This means the total tangential component of gravity must be balanced by the total friction force: $\int_{rope} dm \cdot g \sin\theta = \int_{rope} \mu dm \cdot g \cos\theta$ Since $\lambda = dm/ds$ is the linear mass density and $g$ is constant, and $\mu$ is constant: $\int_{rope} \lambda g \sin\theta ds = \mu \int_{rope} \lambda g \cos\theta ds$ $\int_{rope} \sin\theta ds = \mu \int_{rope} \cos\theta ds$

Now, let's relate these integrals to the given geometry. Let the curve be parameterized such that $x$ is the horizontal coordinate and $y$ is the vertical coordinate. Let the starting point be A and the ending point be B. For an element $ds$ along the curve, the horizontal displacement is $dx = ds \cos\theta$ and the vertical displacement is $dy = ds \sin\theta$.

Integrating these displacements over the entire rope from point A to point B: The total horizontal displacement is $X = \int_{A}^{B} dx = \int_{A}^{B} \cos\theta ds$. The total vertical displacement is $-H = \int_{A}^{B} dy = \int_{A}^{B} \sin\theta ds$. (Note: the vertical displacement is negative because the rope goes downwards).

Substituting these results into the equilibrium condition: $-H = \mu X$ This leads to $\mu = -H/X$, which is physically incorrect as $\mu$, $H$, and $X$ are positive.

Let's re-examine the direction of forces and angles. If we consider the angle $\theta$ such that $dx = ds \cos\theta$ and $dy = ds \sin\theta$, and the rope is going downwards, then $\sin\theta$ is negative.

A more intuitive approach for a uniform rope on a slope: If the rope were a straight line of length $L$ making an angle $\theta$ with the horizontal, then $H = L \sin\theta$ and $X = L \cos\theta$. The condition for impending sliding is $Mg \sin\theta = \mu Mg \cos\theta$, which gives $\mu = \tan\theta$. Since $\tan\theta = \frac{L \sin\theta}{L \cos\theta} = \frac{H}{X}$, for a straight rope, $\mu = \frac{H}{X}$.

For a curved rope, the problem statement implies that the coefficient of friction is uniform along the rope. The condition for impending motion is that the sum of the tangential components of gravity equals the sum of the maximum static friction forces. The result $\mu = H/X$ holds true regardless of the shape of the curve, provided that the friction coefficient is uniform and the system is on the verge of sliding. This can be shown by considering the overall force balance or by more advanced calculus of variations, but for the scope of typical physics problems, the result for a straight line is often generalized. The key is that the net effect of gravity pulling the rope down the slope (represented by the vertical drop $H$) is balanced by the net normal force multiplied by the friction coefficient (related to the horizontal extent $X$).

Therefore, the value of $\mu$ is $\frac{H}{X}$.