Question
Question: A uniform rod of mass m and length l is placed over a smooth horizontal surface along the y-axis and...
A uniform rod of mass m and length l is placed over a smooth horizontal surface along the y-axis and is at rest as shown in the figure an impulsive force F is applied for a small-time Δt along x-direction at a point A. The x-coordinate of the end of the rod when the rod becomes parallel to the x-axis for the first time is: [Initially, the coordinate of the center of mass of the rod is (0,0)]
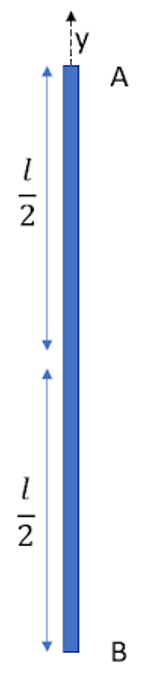
A. 12πl
B. 2l(1+12π)
C. 2l(1−6π)
D. 2l(1+6π)
Solution
As the only force that acts on the body is the impulse, the body will have both linear and angular motion. We will take the axis of rotation as the center of mass and then write expressions for the angular displacement and use that to find the linear displacement of the center of mass.
Formula used:
F.Δt=Δpτ.Δt=ΔL
Complete step-by-step solution:
We know that the torque applied on the rod multiplied by the time for which it is applied gives us the change in angular momentum of the body. Similarly, the product of the force applied to the body and the time for which it is applied gives us the change in linear momentum of the body. So, the linear velocity of the rod will be given as
F.Δt=mv⇒v=mF.Δt
And we will get the angular velocity as
τ.Δt=Iω=12mL2ω⇒ω=mL212×τ.Δt
The angular displacement of the rod will be 2π as the rod goes from being parallel to the y-axis to being parallel to the x-axis as shown in the figure.
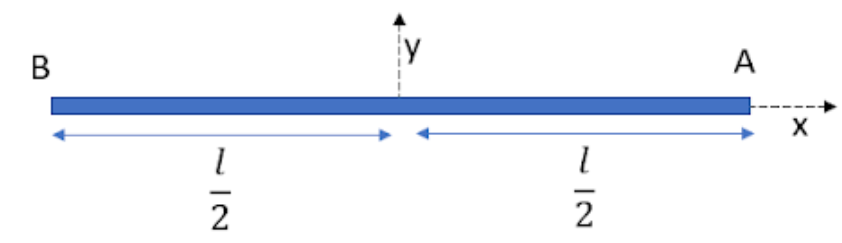
We will find the linear displacement of the centre of mass of the rod in the meantime. Let t be the time the rod takes to become parallel to x-axis for the first time. Then
